Visualizing Datasets¶
Perform one of the following steps to visualize a dataset:
On the Datasets page, select the [Click for Actions] button beside the dataset that you want to view, and then click Visualize from the submenu that appears.
Click the Autoviz top menu link to go to the Visualizations list page, click the New Visualization button, then select or import the dataset that you want to visualize.
The Visualization page shows all available graphs for the selected dataset. Note that the graphs on the Visualization page can vary based on the information in your dataset. You can also view and download logs that were generated during the visualization.
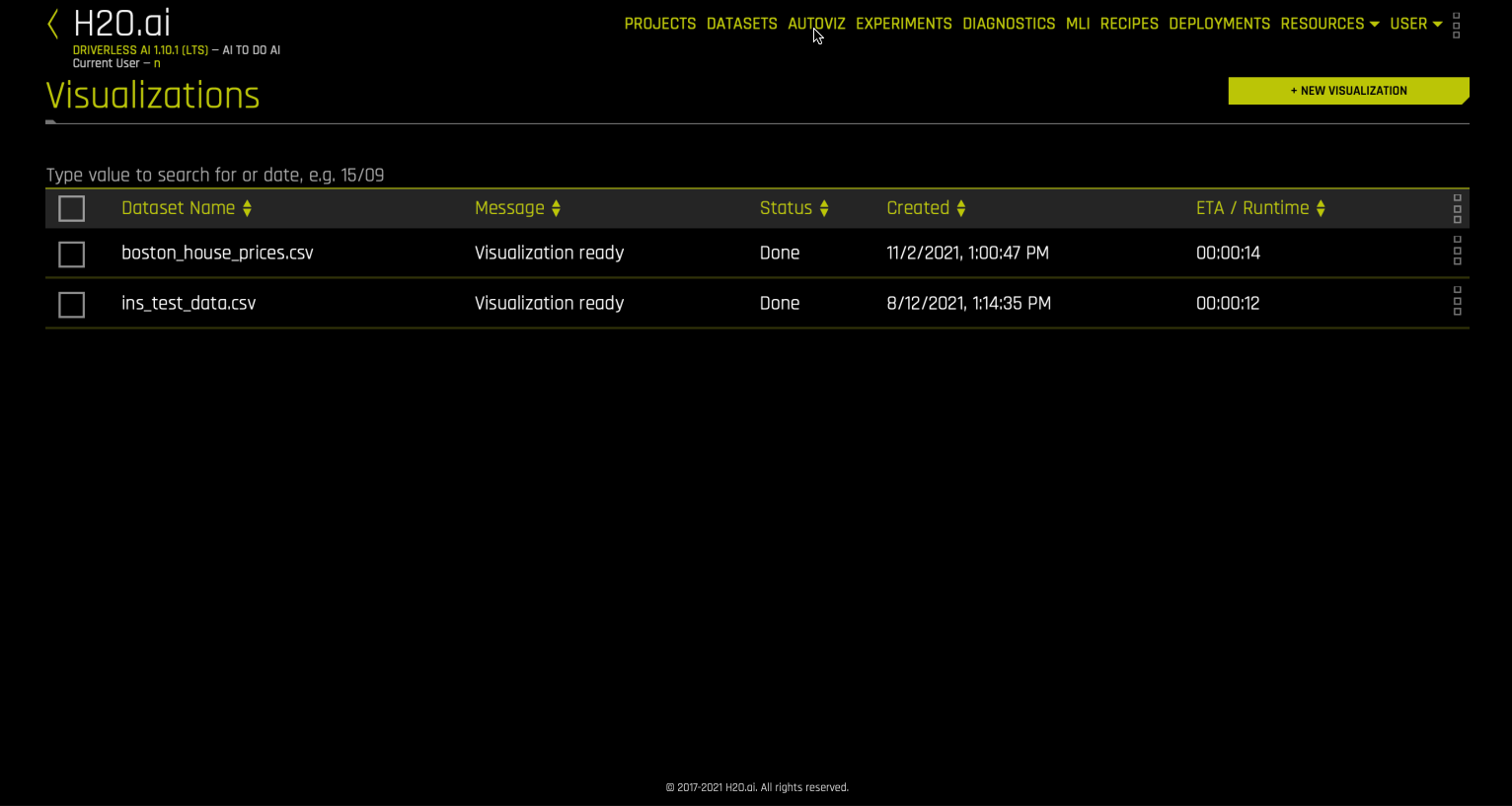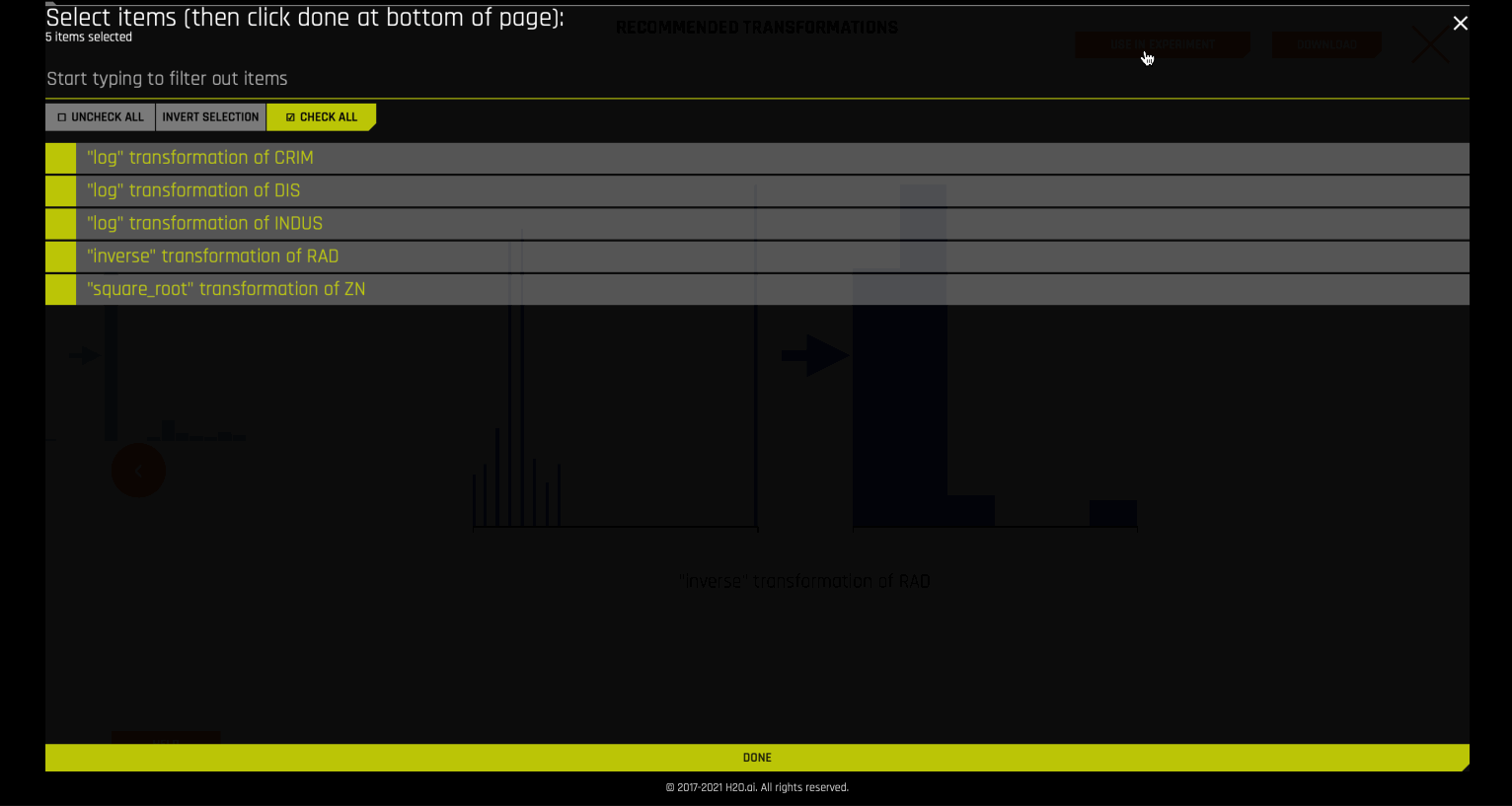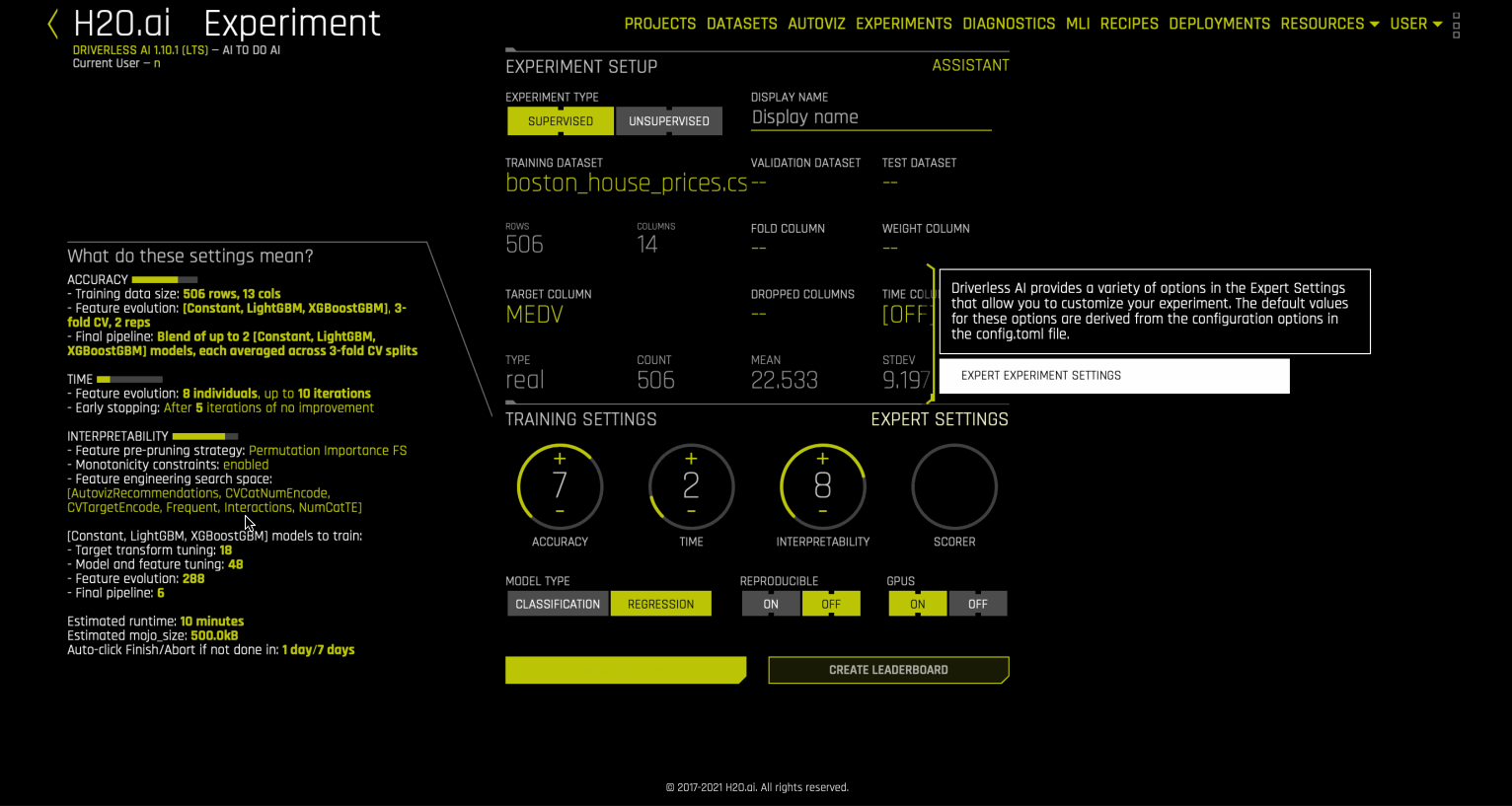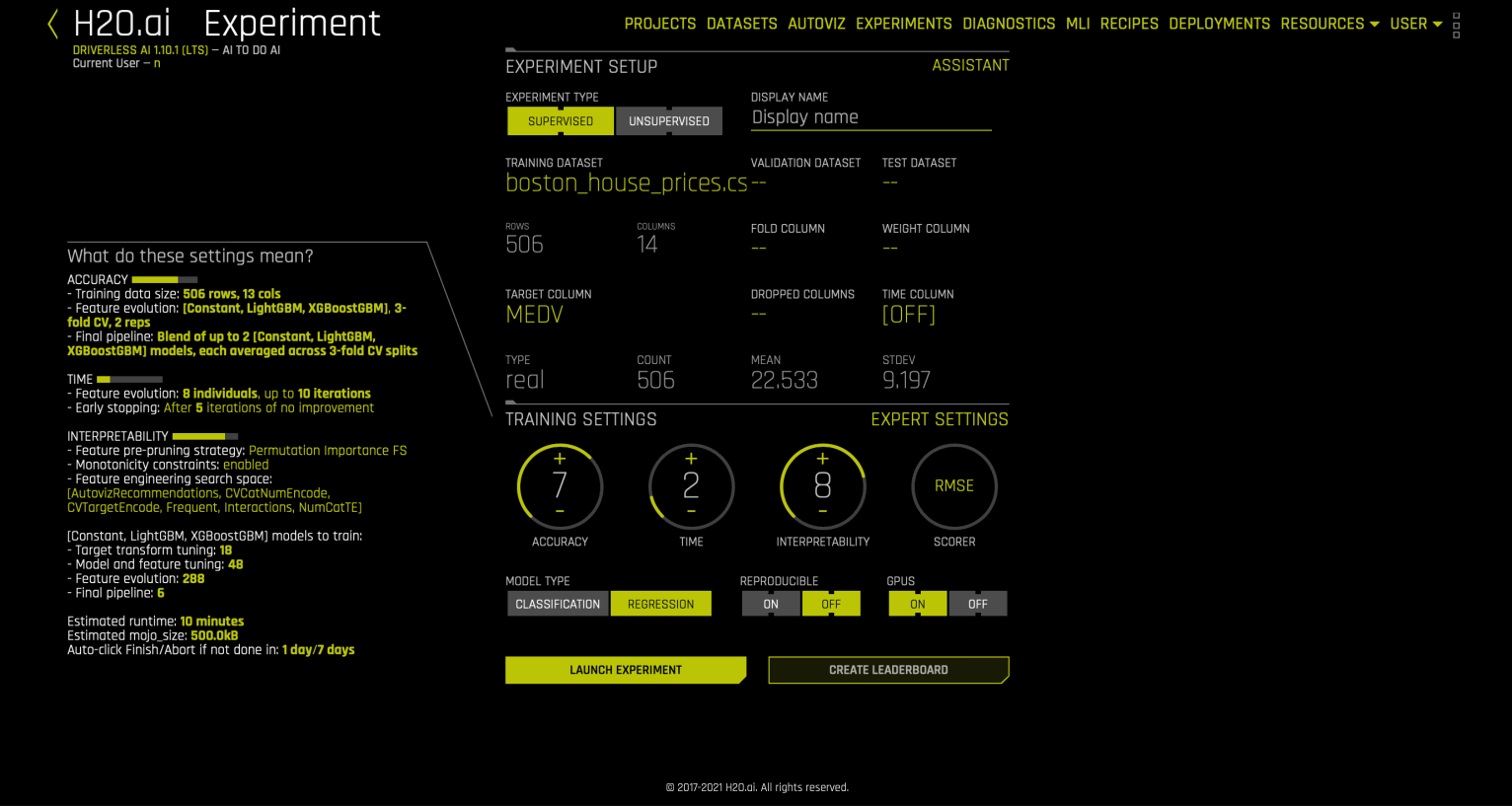
Autoviz Recommendations¶
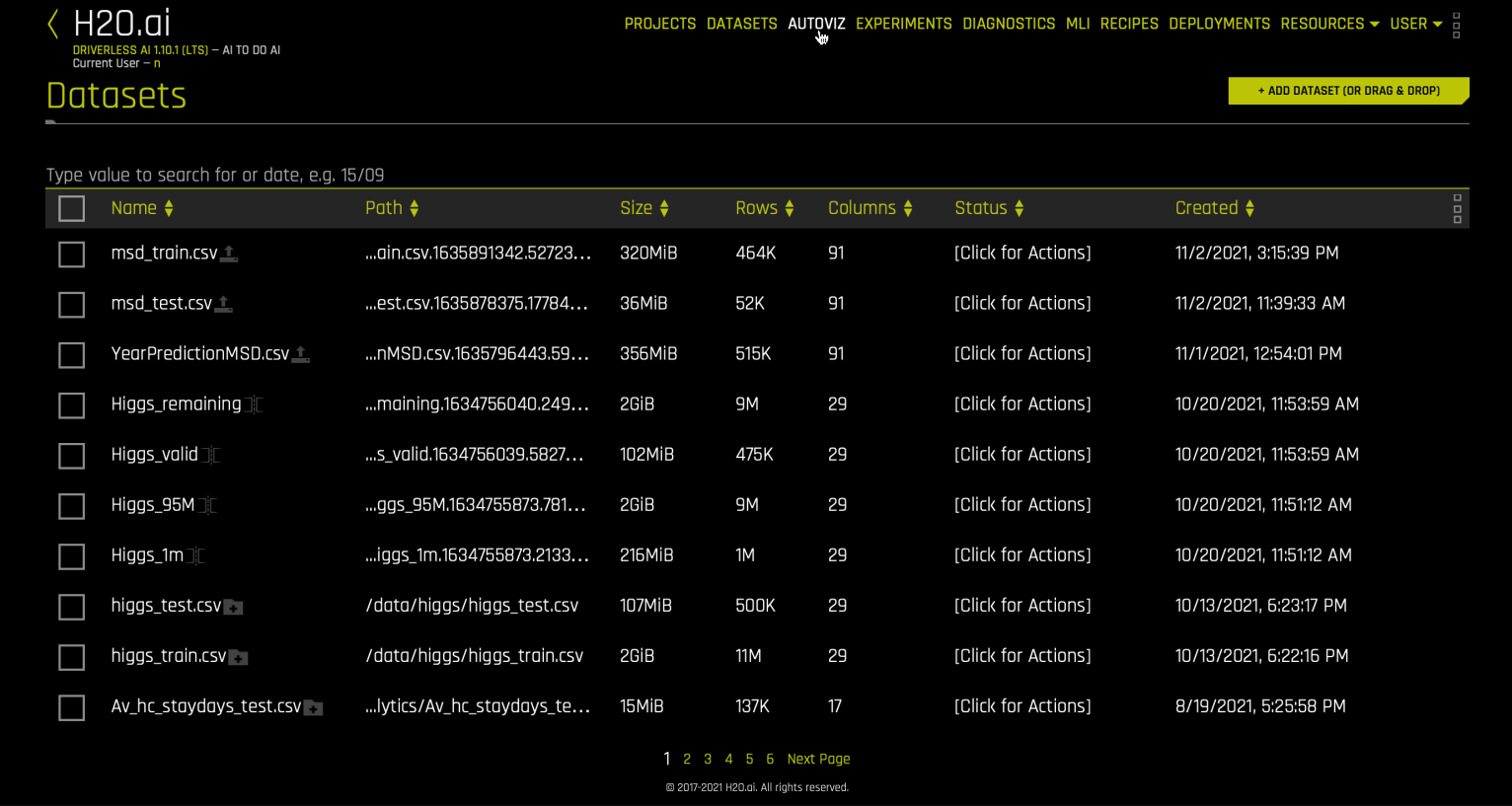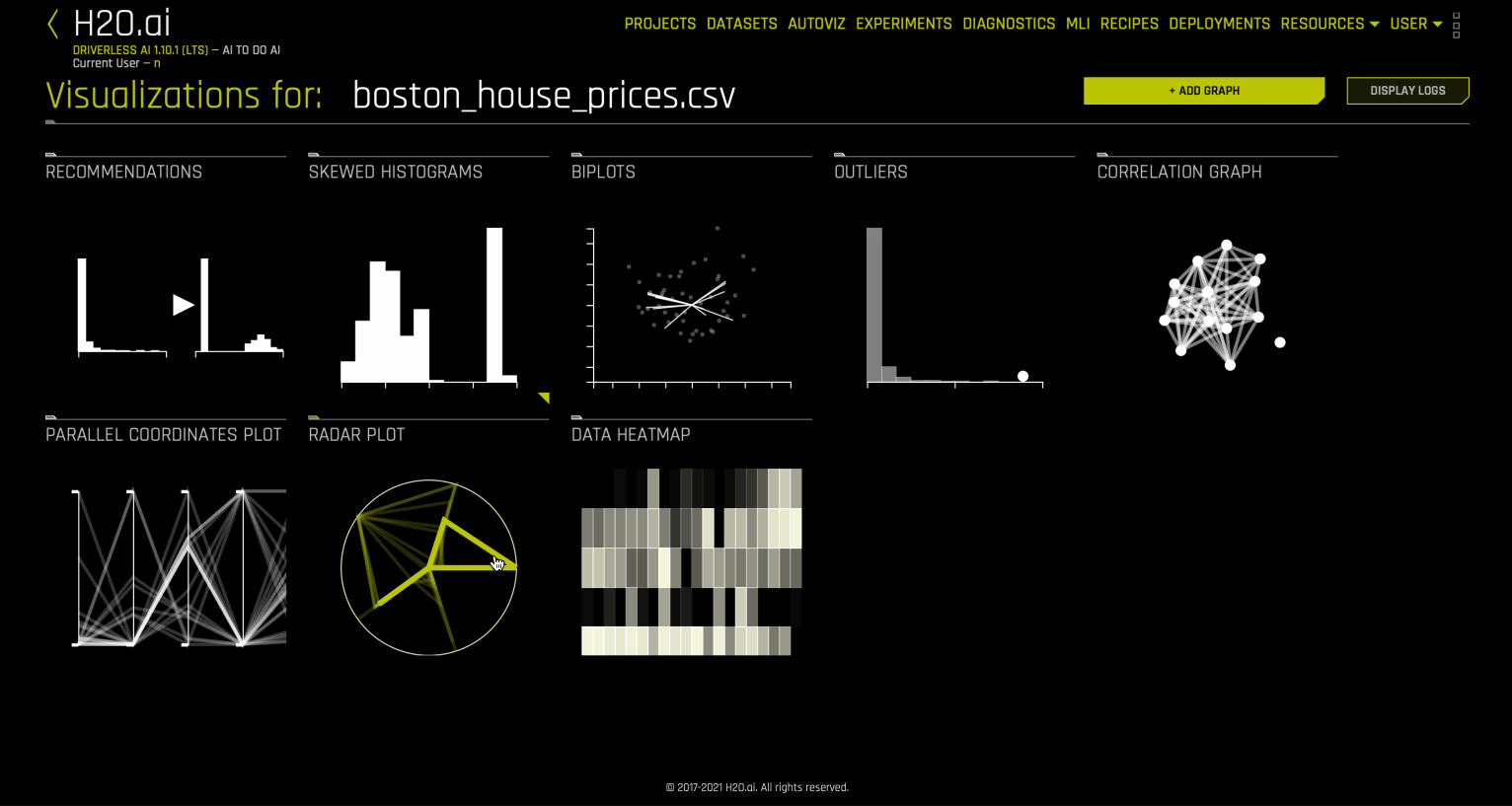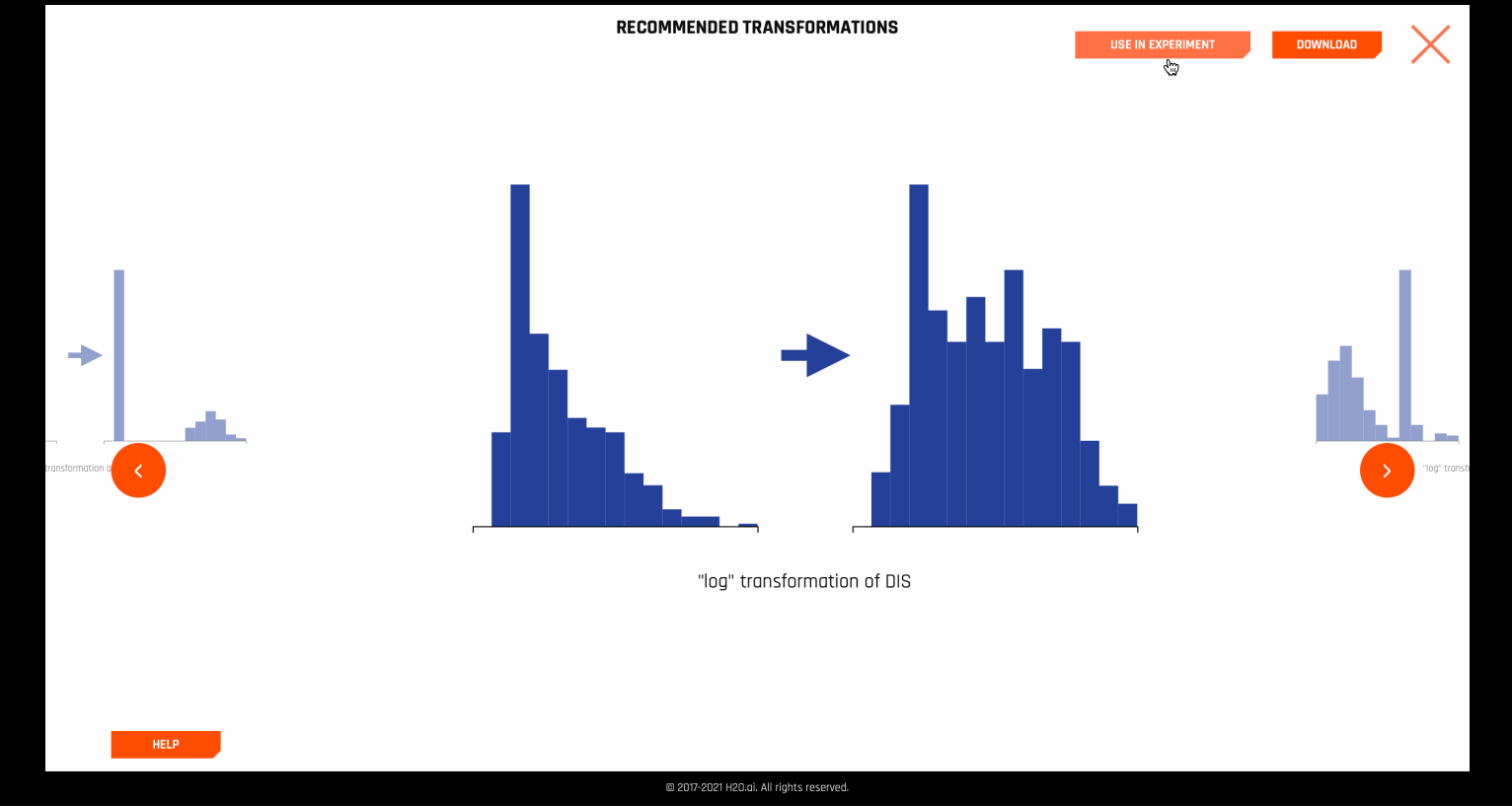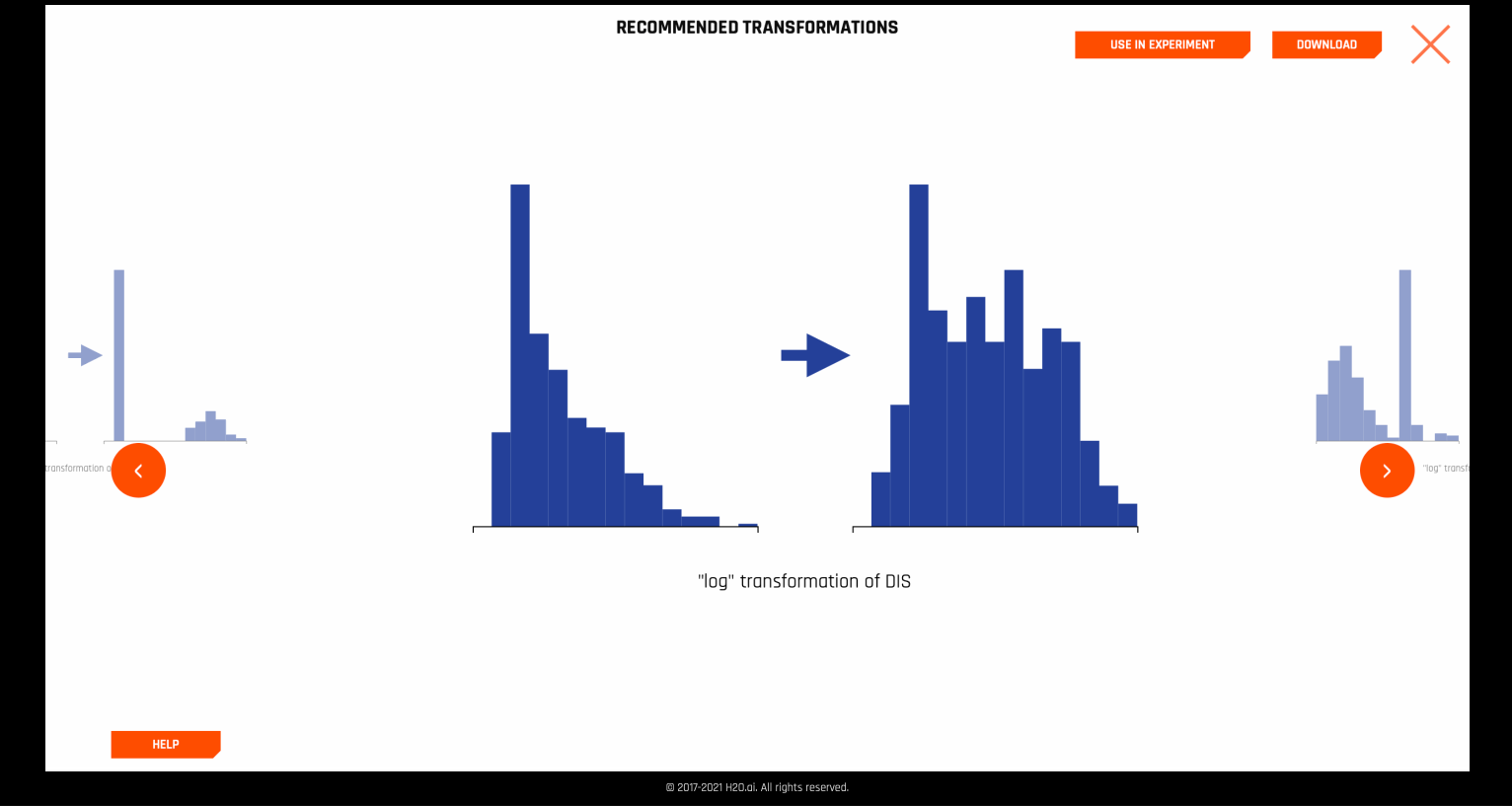
For some cases, Autoviz suggests certain recommended transformations to the columns of the dataset.
These recommendations can be directly applied to the experiment. This is done internally by using the autoviz recommendation transformer.
The following is a complete list of available graphs from Driverless AI Autoviz.
Spikey Histograms¶
Spikey histograms are histograms with huge spikes. This often indicates an inordinate number of single values (usually zeros) or highly similar values. The measure of “spikeyness” is a bin frequency that is ten times the average frequency of all the bins. You should be careful when modeling (particularly regression models) with spikey variables.
Skewed Histograms¶
Skewed histograms are ones with especially large skewness (asymmetry). The robust measure of skewness is derived from Groeneveld, R.A. and Meeden, G. (1984), “Measuring Skewness and Kurtosis.” The Statistician, 33, 391-399. Highly skewed variables are often candidates for a transformation (e.g., logging) before use in modeling. The histograms in the output are sorted in descending order of skewness.
Varying Boxplots¶
Varying boxplots reveal unusual variability in a feature across the categories of a categorical variable. The measure of variability is computed from a robust one-way analysis of variance (ANOVA). Sufficiently diverse variables are flagged in the ANOVA. A boxplot is a graphical display of the fractiles of a distribution. The center of the box denotes the median, the edges of a box denote the lower and upper quartiles, and the ends of the “whiskers” denote that range of values. Sometimes outliers occur, in which case the adjacent whisker is shortened to the next lower or upper value. For variables (features) having only a few values, the boxes can be compressed, sometimes into a single horizontal line at the median.
Heteroscedastic Boxplots¶
Heteroscedastic boxplots reveal unusual variability in a feature across the categories of a categorical variable. Heteroscedasticity is calculated with a Brown-Forsythe test: Brown, M. B. and Forsythe, A. B. (1974), “Robust tests for equality of variances. Journal of the American Statistical Association, 69, 364-367. Plots are ranked according to their heteroscedasticity values. A boxplot is a graphical display of the fractiles of a distribution. The center of the box denotes the median, the edges of a box denote the lower and upper quartiles, and the ends of the “whiskers” denote that range of values. Sometimes outliers occur, in which case the adjacent whisker is shortened to the next lower or upper value. For variables (features) having only a few values, the boxes can be compressed, sometimes into a single horizontal line at the median.
Biplots¶
A Biplot is an enhanced scatterplot that uses both points and vectors to represent structure simultaneously for rows and columns of a data matrix. Rows are represented as points (scores), and columns are represented as vectors (loadings). The plot is computed from the first two principal components of the correlation matrix of the variables (features). You should look for unusual (non-elliptical) shapes in the points that might reveal outliers or non-normal distributions. And you should look for purple vectors that are well-separated. Overlapping vectors can indicate a high degree of correlation between variables.
Outliers¶
Variables with anomalous or outlying values are displayed as red points in a dot plot. Dot plots are constructed using an algorithm in Wilkinson, L. (1999). “Dot plots.” The American Statistician, 53, 276–281. Not all anomalous points are outliers. Sometimes the algorithm will flag points that lie in an empty region (i.e., they are not near any other points). You should inspect outliers to see if they are miscodings or if they are due to some other mistake. Outliers should ordinarily be eliminated from models only when there is a reasonable explanation for their occurrence.
Correlation Graph¶
The correlation network graph is constructed from all pairwise squared correlations between variables (features). For continuous-continuous variable pairs, the statistic used is the squared Pearson correlation. For continuous-categorical variable pairs, the statistic is based on the squared intraclass correlation (ICC). This statistic is computed from the mean squares from a one-way analysis of variance (ANOVA). The formula is (MSbetween - MSwithin)/(MSbetween + (k - 1)MSwithin), where k is the number of categories in the categorical variable. For categorical-categorical pairs, the statistic is computed from Cramer’s V squared. If the first variable has k1 categories and the second variable has k2 categories, then a k1 x k2 table is created from the joint frequencies of values. From this table, we compute a chi-square statistic. Cramer’s V squared statistic is then (chi-square / n) / min(k1,k2), where n is the total of the joint frequencies in the table. Variables with large values of these respective statistics appear near each other in the network diagram. The color scale used for the connecting edges runs from low (blue) to high (red). Variables connected by short red edges tend to be highly correlated.
Parallel Coordinates Plot¶
A Parallel Coordinates Plot is a graph used for comparing multiple variables. Each variable has its own vertical axis in the plot. Each profile connects the values on the axes for a single observation. If the data contain clusters, these profiles will be colored by their cluster number.
Radar Plot¶
A Radar Plot is a two-dimensional graph that is used for comparing multiple variables. Each variable has its own axis that starts from the center of the graph. The data are standardized on each variable between 0 and 1 so that values can be compared across variables. Each profile, which usually appears in the form of a star, connects the values on the axes for a single observation. Multivariate outliers are represented by red profiles. The Radar Plot is the polar version of the popular Parallel Coordinates plot. The polar layout enables us to represent more variables in a single plot.
Data Heatmap¶
The heatmap graphic is constructed from the transposed data matrix. Rows of the heatmap represent variables, and columns represent cases (instances). The data are standardized before display so that small values are yellow and large values are red. The rows and columns are permuted via a singular value decomposition (SVD) of the data matrix so that similar rows and similar columns are near each other.
Recommendations¶
The recommendations graphic implements the Tukey ladder of powers collection of log, square root, and inverse data transformations described in Exploratory Data Analysis (Tukey, 1977). Also implemented are extensions of these three transformers that handle negative values, which are derived from I.K. Yeo and R.A. Johnson, “A new family of power transformations to improve normality or symmetry.” Biometrika, 87(4), (2000). For each transformer, transformations are selected by comparing the robust skewness of the transformed column with the robust skewness of the original raw column. When a transformation leads to a relatively low value of skewness, it is recommended.
Missing Values Heatmap¶
The missing values heatmap graphic is constructed from the transposed data matrix. Rows of the heatmap represent variables and columns represent cases (instances). The data are coded into the values 0 (missing) and 1 (nonmissing). Missing values are colored red and nonmissing values are left blank (white). The rows and columns are permuted via a singular value decomposition (SVD) of the data matrix so that similar rows and similar columns are near each other.
Gaps Histogram¶
The gaps index is computed using an algorithm of Wainer and Schacht based on work by John Tukey. (Wainer, H. and Schacht, Psychometrika, 43, 2, 203-12.) Histograms with gaps can indicate a mixture of two or more distributions based on possible subgroups not necessarily characterized in the dataset.
The images on this page are thumbnails. You can click on any of the graphs to view and download a full-scale image. You can also view an explanation for each graph by clicking the Help button in the lower-left corner of each expanded graph.