将数据集可视化¶
执行以下步骤之一即可将数据集可视化:
在“数据集”页面,选择您想要查看的数据集旁的 [点击操作] 按钮,然后在显示的子菜单中点击 可视化 。
点击 Autoviz 顶部菜单链接,转至“可视化”列表页面,点击 新建可视化 按钮,然后选择或导入您想要可视化的数据集。
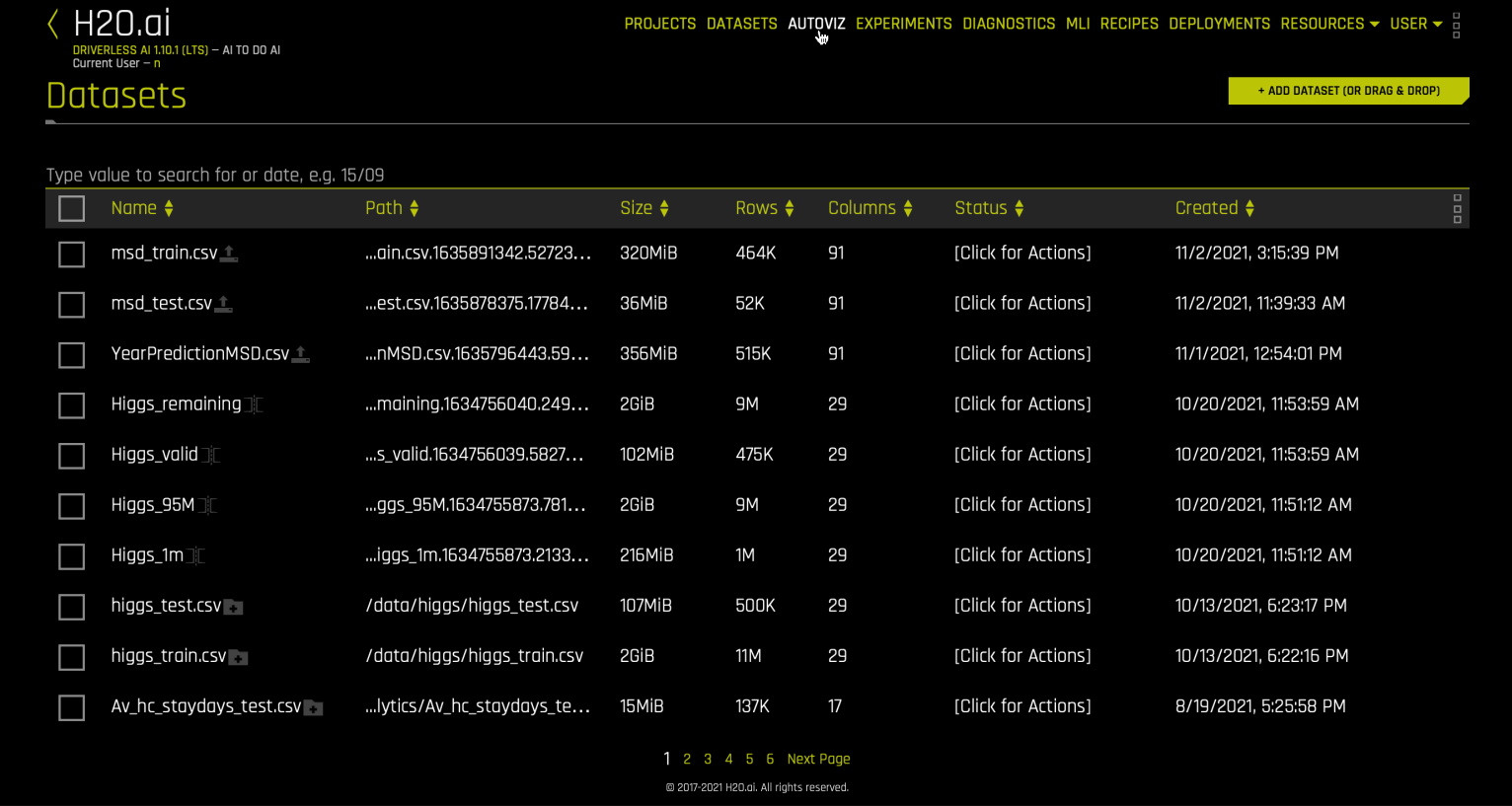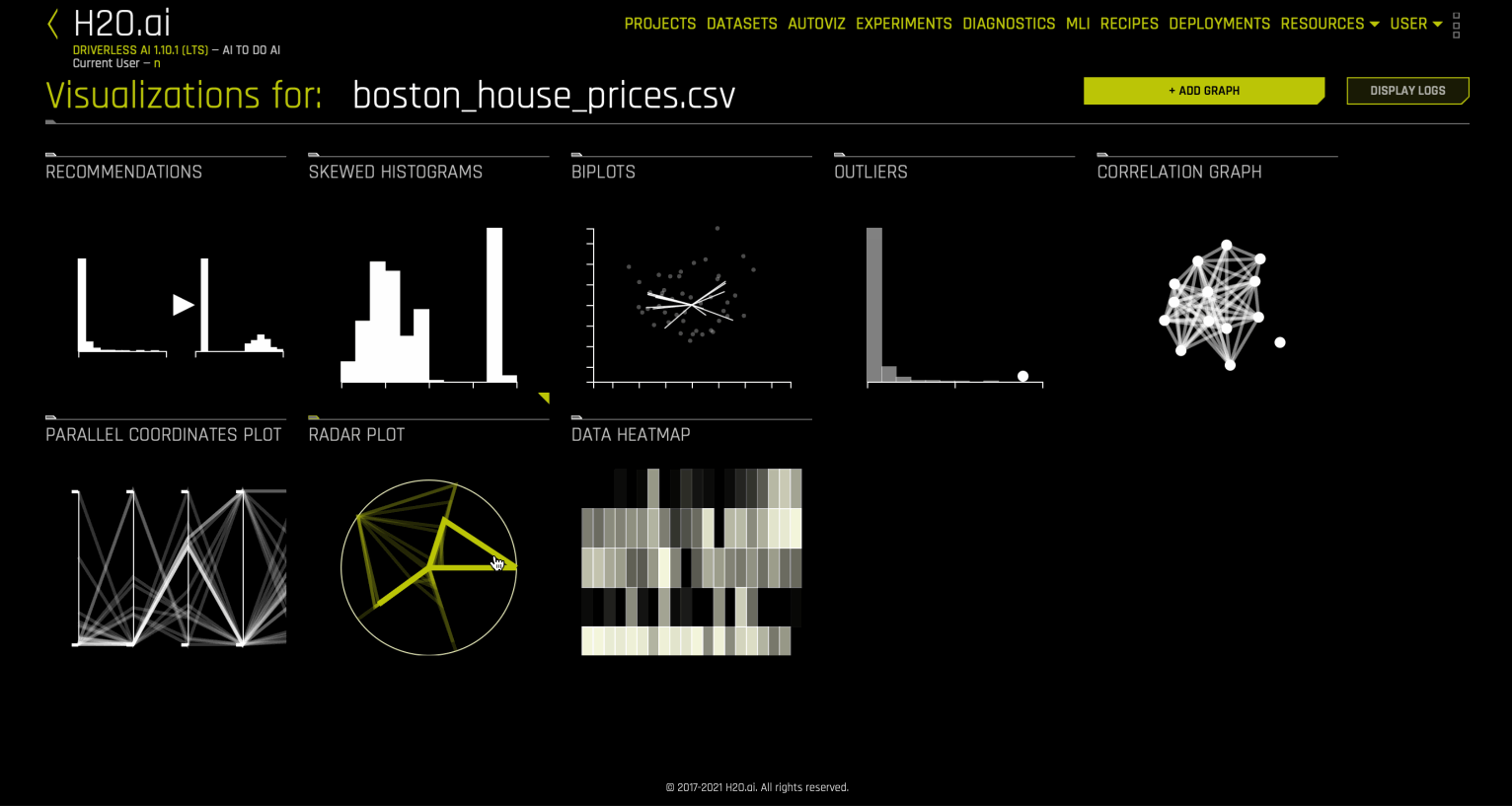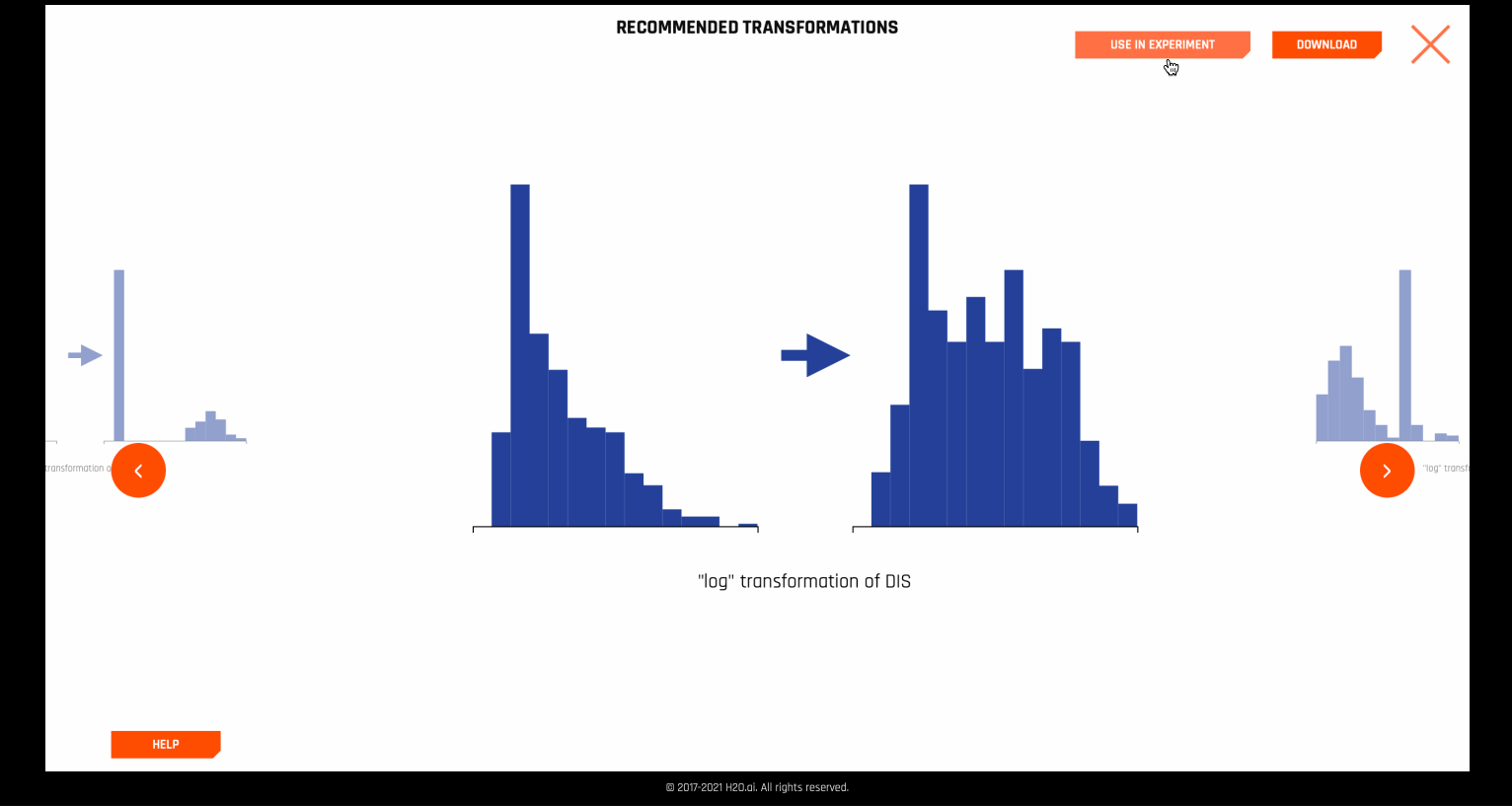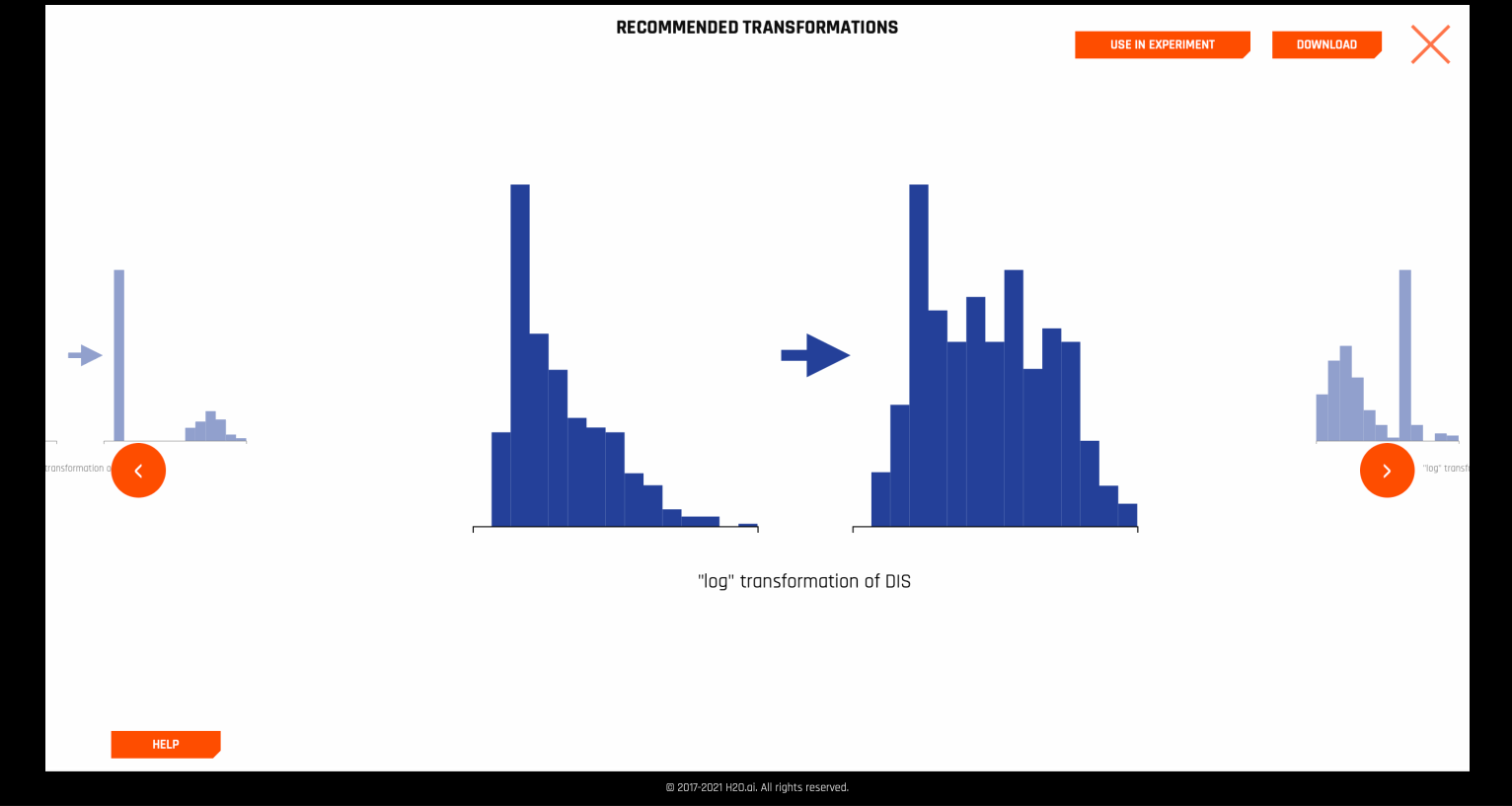
“可视化”页面显示了可用于所选数据集的所有图表。请注意,“可视化”页面的图表可能会因为数据集中的信息而异。您还可以查看和下载可视化过程中生成的日志。
Autoviz 推荐¶
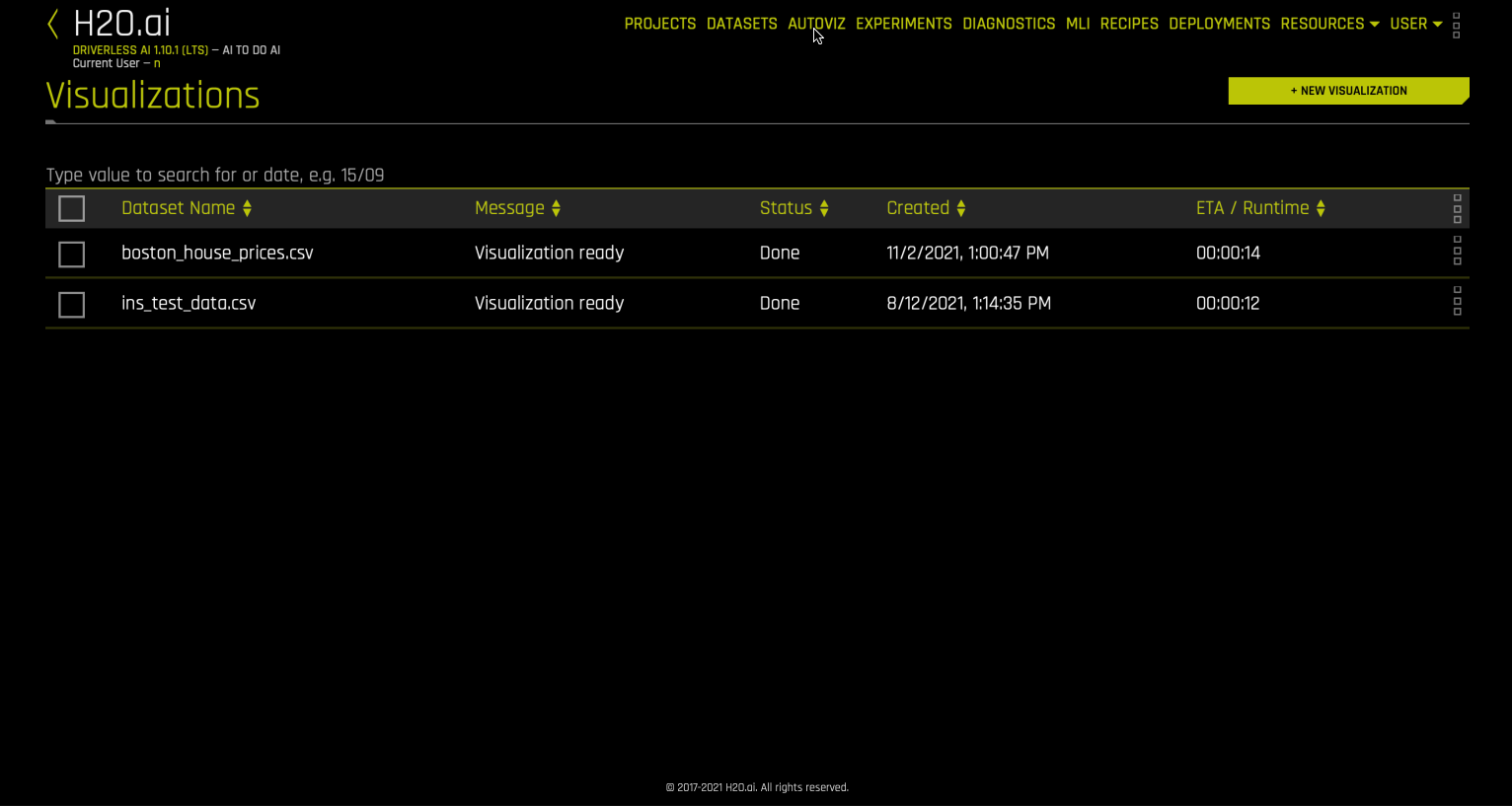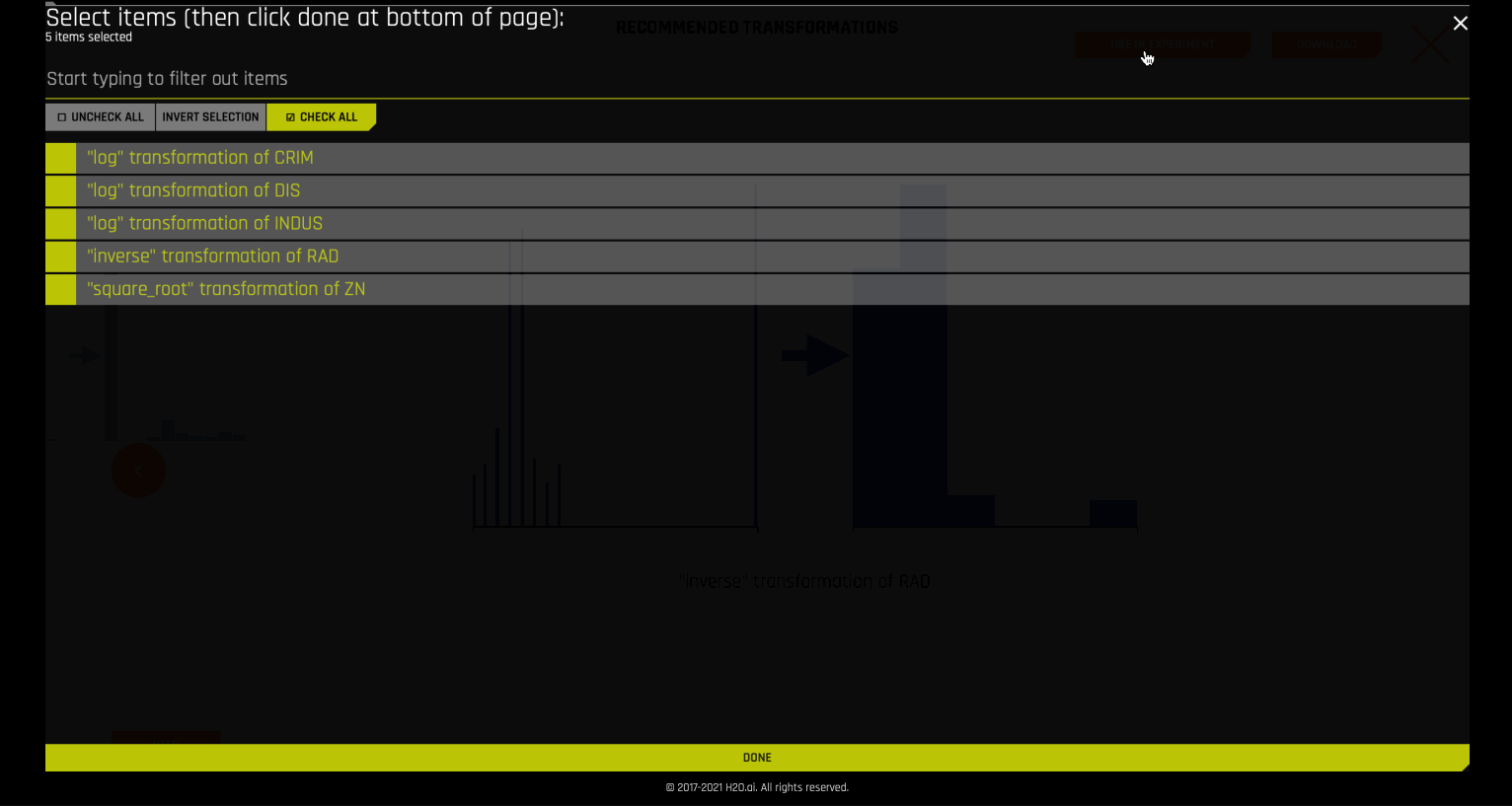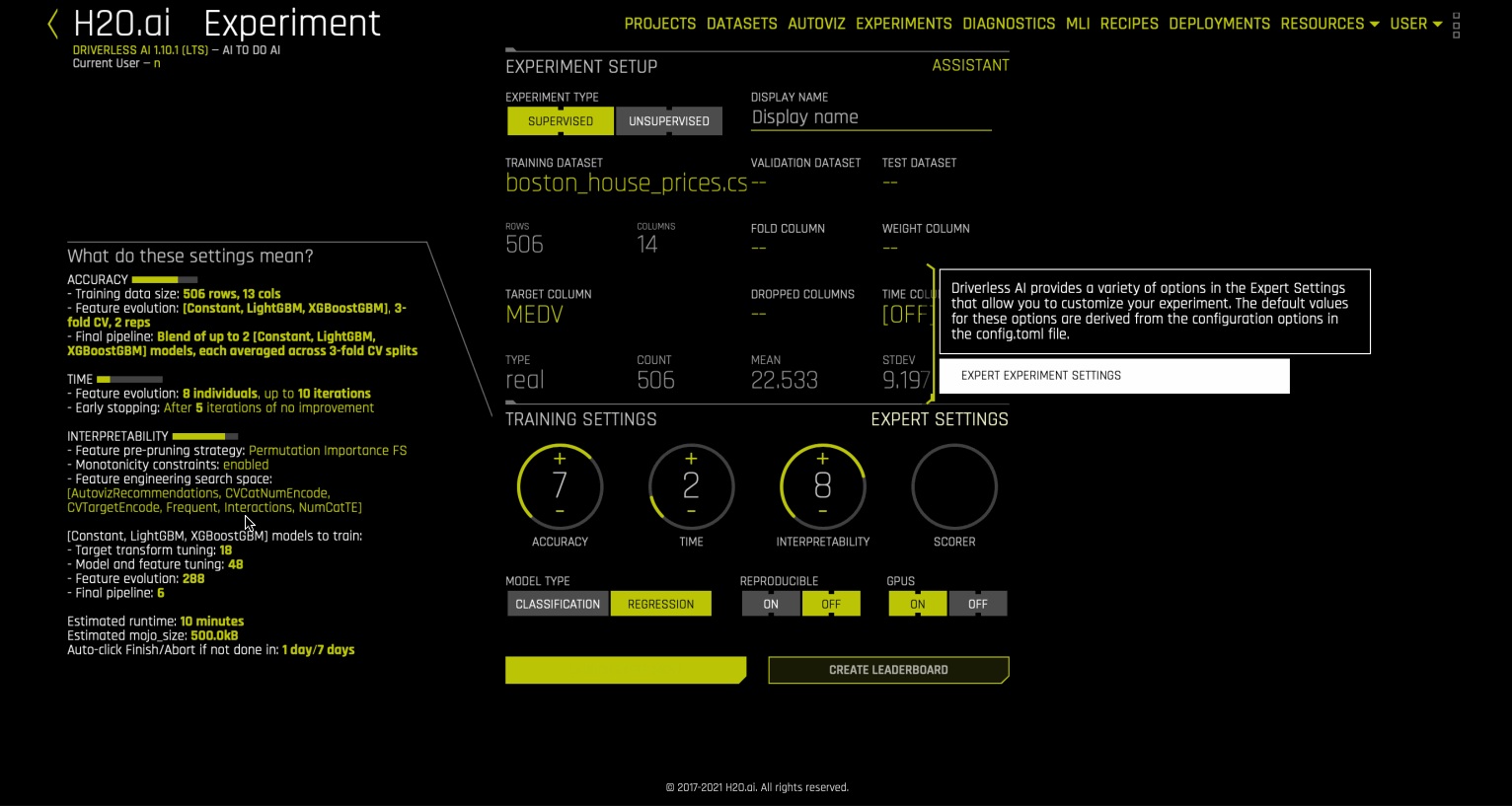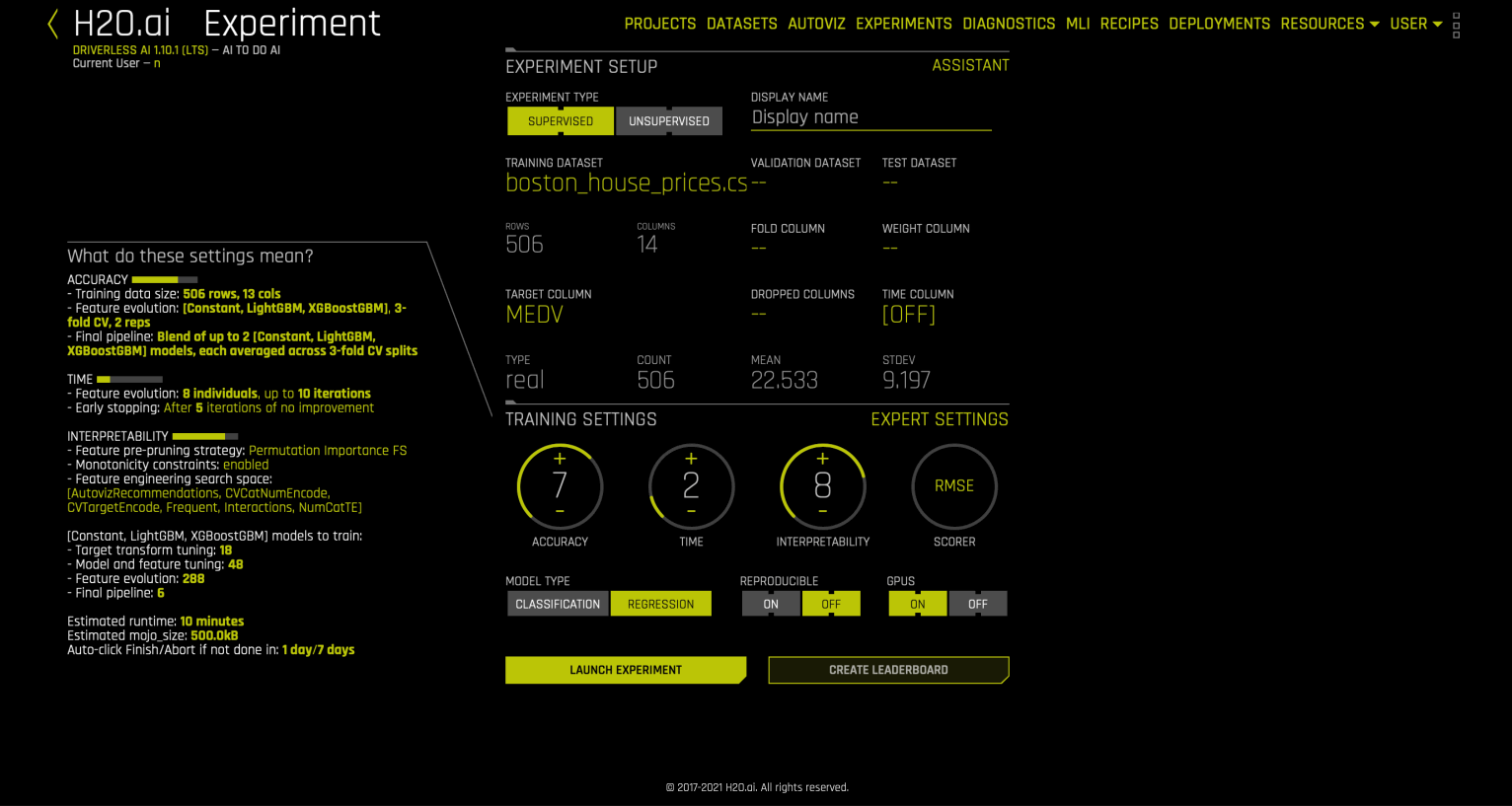
在某些情况下,Autoviz 建议对数据集列进行某些推荐的变量转换。
这些推荐可直接应用于实验。若要在内部完成此操作,可使用 autoviz recommendation transformer.
以下是 Driverless AI Autoviz 中可用图表的完整列表。
Spikey 直方图¶
Spikey 直方图是呈现巨大尖峰的直方图。这通常表明单个值(通常为零)或高度相似的值数量过多。”spikeyness”通过分箱频率衡量,此频率是所有分箱平均频率的十倍。在使用 spikey 变量建模(特别是回归模型)时,您应该多加注意。
偏斜直方图¶
偏斜直方图是偏斜度(不对称性)极大的直方图。偏斜度的有效衡量指标源自于 Groeneveld, R.A. and Meeden, G. (1984), “Measuring Skewness and Kurtosis.” The Statistician, 33, 391-399。高度偏斜的变量通常要在用于建模前进行转换(例如,日志记录)。所输出的直方图将按偏斜度降序排序。
可变箱形图¶
可变箱形图揭示了分类变量类别中某个特征的异常可变性。可变性通过稳健的单因素方差分析 (ANOVA) 计算得出。ANOVA 中标记了足够多样化的变量。箱形图以图形方式显示了分布的分位数。箱子的中心表示中位数,其边缘表示下四分位数和上四分位数,”须线”的两端表示值的范围。当出现异常值时,相邻须线将缩短至下一个低值或高值。对于仅有几个值的变量(特征),可以将箱子进行压缩,有时可压缩为中位数处的一条水平线。
异方差箱形图¶
异方差箱形图揭示了分类变量类别中特征的异常可变性。异方差性通过 Brown-Forsythe 检验计算得出:Brown, M. B. and Forsythe, A. B. (1974), “Robust tests for equality of variances. Journal of the American Statistical Association, 69, 364-367。这些箱形图将根据异方差性的值进行排序。箱形图以图形方式显示了分布的分位数。箱子的中心表示中位数,其边缘表示下四分位数和上四分位数,”须线”的两端表示值的范围。当出现异常值时,相邻须线将缩短至下一个低值或高值。对于仅有几个值的变量(特征),可以将箱子进行压缩,有时可压缩为中位数处的一条水平线。
双标图¶
双标图是增强型的散点图,使用点和向量来表示数据矩阵中行和列的结构。行用点(评分)表示,列用向量(加载项)表示。双标图通过变量(特征)相关矩阵的前两个主分量计算得出。您应该在可能显示异常值或非正态分布的点中寻找异常(非椭圆形)形状。并且您应该寻找完全分离的紫色向量。重叠的向量表明变量之间存在高度相关性。
异常值¶
在点图中,具有异常值或离群值的变量显示为红点。点图使用一种算法(参见 Wilkinson, L. (1999). “Dot plots.” The American Statistician, 53, 276–281)构建。但并非所有异常的点都是异常值。有时,算法会标记位于空白区域的点(即,这些点不靠近任何其他点)。您应该检查异常值,了解它们是否属于错误编码或是否是由其他一些错误引起。通常,只有在能合理解释异常值出现的原因时,方可从模型中剔除异常值。
相关性图¶
相关性网络图是由变量(特征)之间所有成对的平方相关关系构建而成。对于连续-连续变量对,所使用的统计量是皮尔逊相关系数平方值。对于连续-分类变量,统计量则基于组内相关系数 (ICC) 的平方值。此统计量根据单因素方差分析 (ANOVA) 中的均方计算得出。公式为 (MSbetween - MSwithin)/(MSbetween + (k - 1)Mswithin),其中 k 是分类变量的类别数。对于分类-分类对,统计量根据克莱姆 V 系数的平方值计算得出。如果第一个变量有 k1 个类别且第二个变量有 k2 个类别,则将根据值的联合频率创建 k1 x k2 表。在此表中,我们可计算卡方统计量。因此,克莱姆 V 系数的平方统计量为:(chi-square / n) / min(k1,k2),其中 n 是表中联合频率的总和。各自统计量中值较大的变量在网络图中会相互靠近。用于连接边缘的色阶从最小值(蓝色)变化到最大值(红色)。由红色短边连接的变量往往具有高度相关性。
平行座标图¶
平行座标图用于比较多个变量。每个变量在图中均有自己的纵坐标。而每个剖面均将坐标轴上的值连接起来,以进行单次观测。如果数据中含有聚类,则这些剖面可根据其聚类编号进行着色。
雷达图¶
雷达图是用于比较多个变量的二维图表。每个变量均有自己的轴,轴可以从图表的中心位置开始。针对 0 和 1 之间的每个变量,数据将被标准化,因而可以在变量之间对值进行比较。每个剖面(通常以星形显示)均连接坐标轴上的值,以进行单次观测。多元异常值以红色剖面呈现。雷达图是普遍使用的平行坐标图的极坐标版本。极坐标布局让我们能够在单个图例中显示更多的变量。
数据热图¶
热图由转置的数据矩阵构建而成。热图中的行表示变量,列表示用例(实例)。数据在显示前已被标准化,因此小值为黄色,大值为红色。行和列均通过数据矩阵的奇异值分解 (SVD) 进行排序,以使相似行和相似列相互靠近。
建议图表¶
建议实现了*探索性数据分析* (Tukey, 1977) 中所述的对数、平方根和逆数据转换的 Tukey 幂阶集合。此外,还实现了以上三种处理负值的转换器的扩展,参见 I.K. Yeo and R.A. Johnson, “A new family of power transformations to improve normality or symmetry.” Biometrika, 87(4), (2000)。对于每个转换器,通过比较转换后的列的稳健偏斜度和原始列的稳健偏斜度来选择转换。当转换可使偏斜度值相对较低时,建议使用此方法。
缺失值热图¶
缺失值热图由转置的数据矩阵构建而成。热图中的行表示变量,列表示用例(实例)。数据被编码为值 0(缺失)和 1(非缺失)。缺失值用红色表示,而非缺失值则保留为空白(白色)。行和列均通过数据矩阵的奇异值分解 (SVD) 进行排序,以使相似行和相似列相互靠近。
间隔直方图¶
间隔指数使用基于 John Tukey 著作的 Wainer 和 Schacht 算法计算 (Wainer, H. and Schacht, Psychometrika, 43, 2, 203-12)。带有间隔的直方图可同时呈现两个或多个基于可能子分组(在数据集中不一定有表征)的分布。
本页面上的图片均为缩略图。您可以点击任意图表以查看和下载完整尺寸的图表。您还可通过点击每个展开图表左下角的 帮助 按钮查看每个图表的解释。