세이터 세트 시각화¶
다음 단계 중 하나를 수행하여 데이터 세트를 시각화하십시오.
데이터 세트 페이지에서 확인하려는 데이터 세트 옆에 위치한 [Click for Actions] 버튼을 선택한 후, 표시되는 하위 메뉴에서 Visualize 를 클릭하십시오.
Autoviz 상단 메뉴의 링크를 클릭하여 시각화 목록 페이지로 이동한 후, New Visualization 버튼을 클릭하고 시각화할 데이터 세트를 선택하거나 가져옵니다.
시각화 페이지에는 선택한 데이터 세트에 사용 가능한 모든 그래프가 표시됩니다. 시각화 페이지 상의 그래프는 데이터 세트의 정보에 따라 달라질 수 있습니다. 시각화 중에 생성된 로그를 확인하여 다운로드할 수도 있습니다.
Autoviz 권장 사항¶
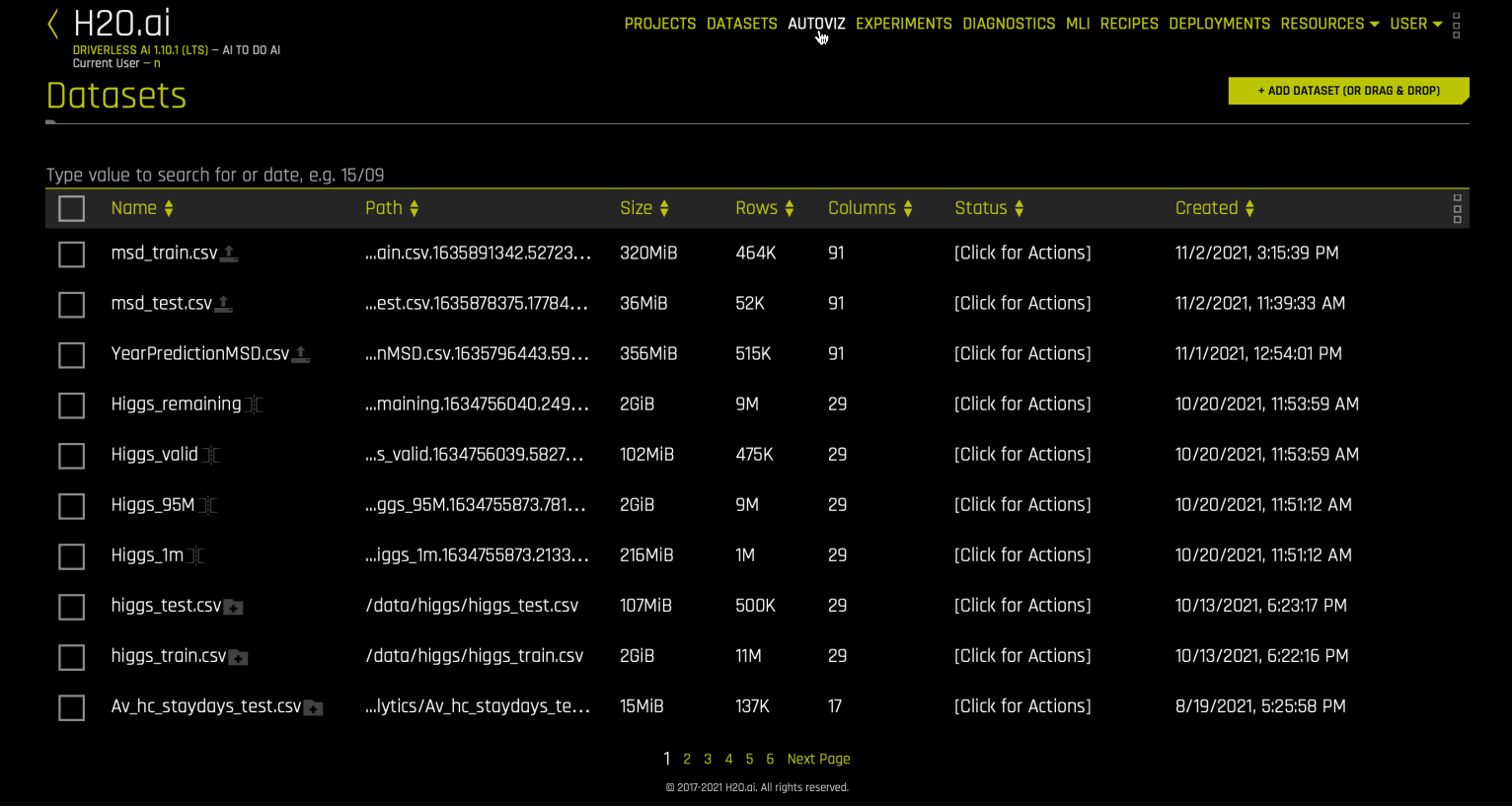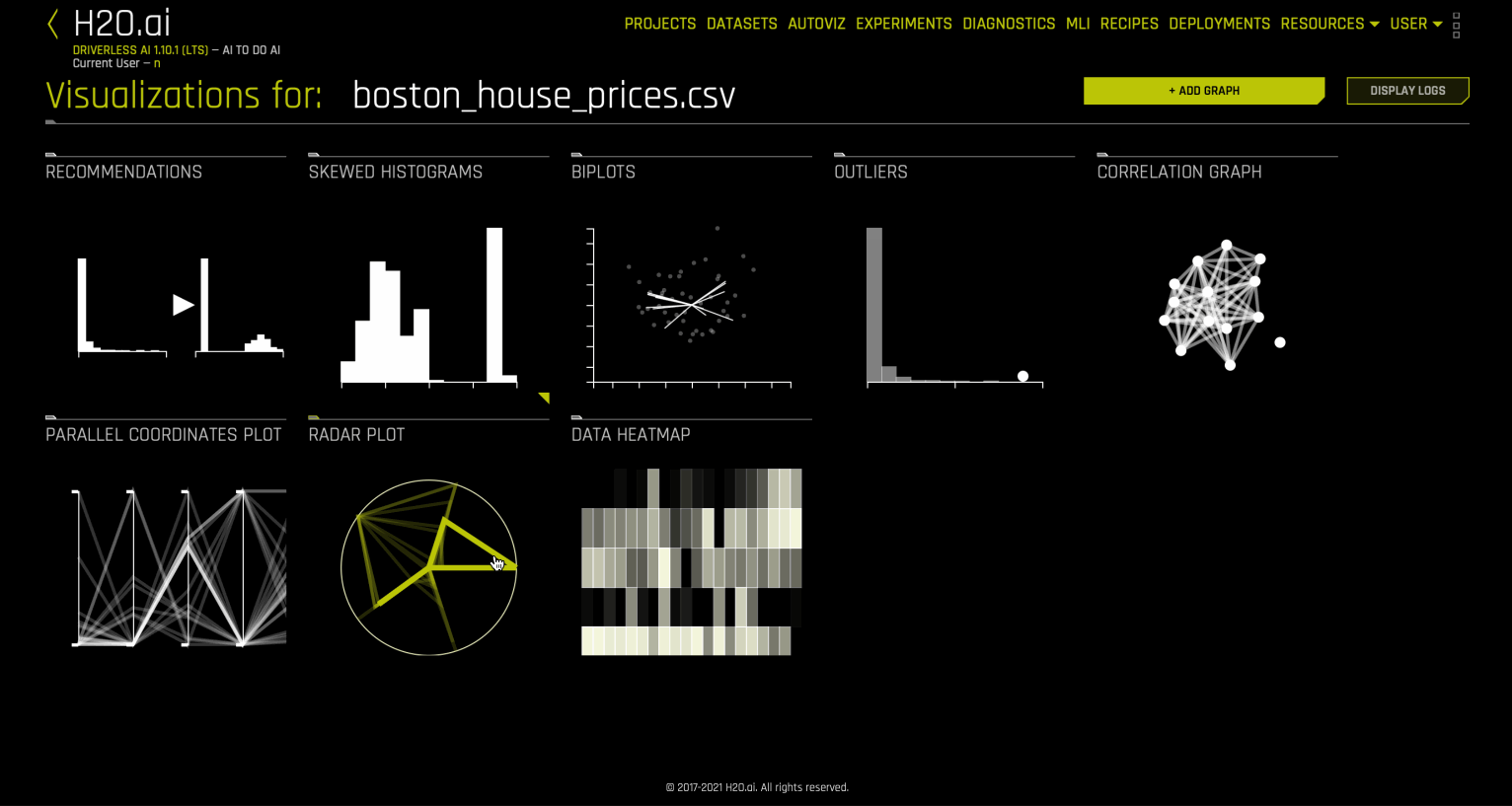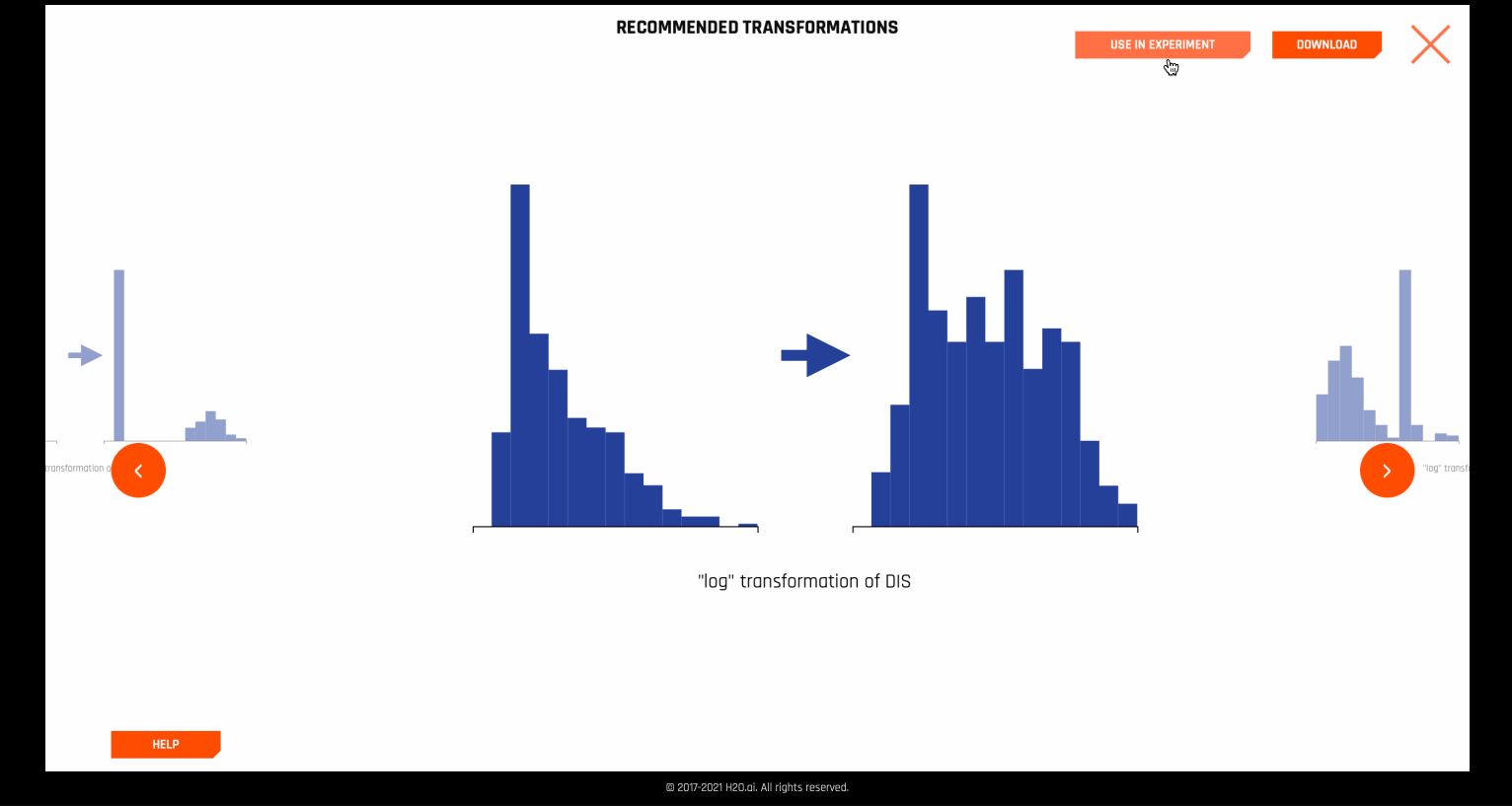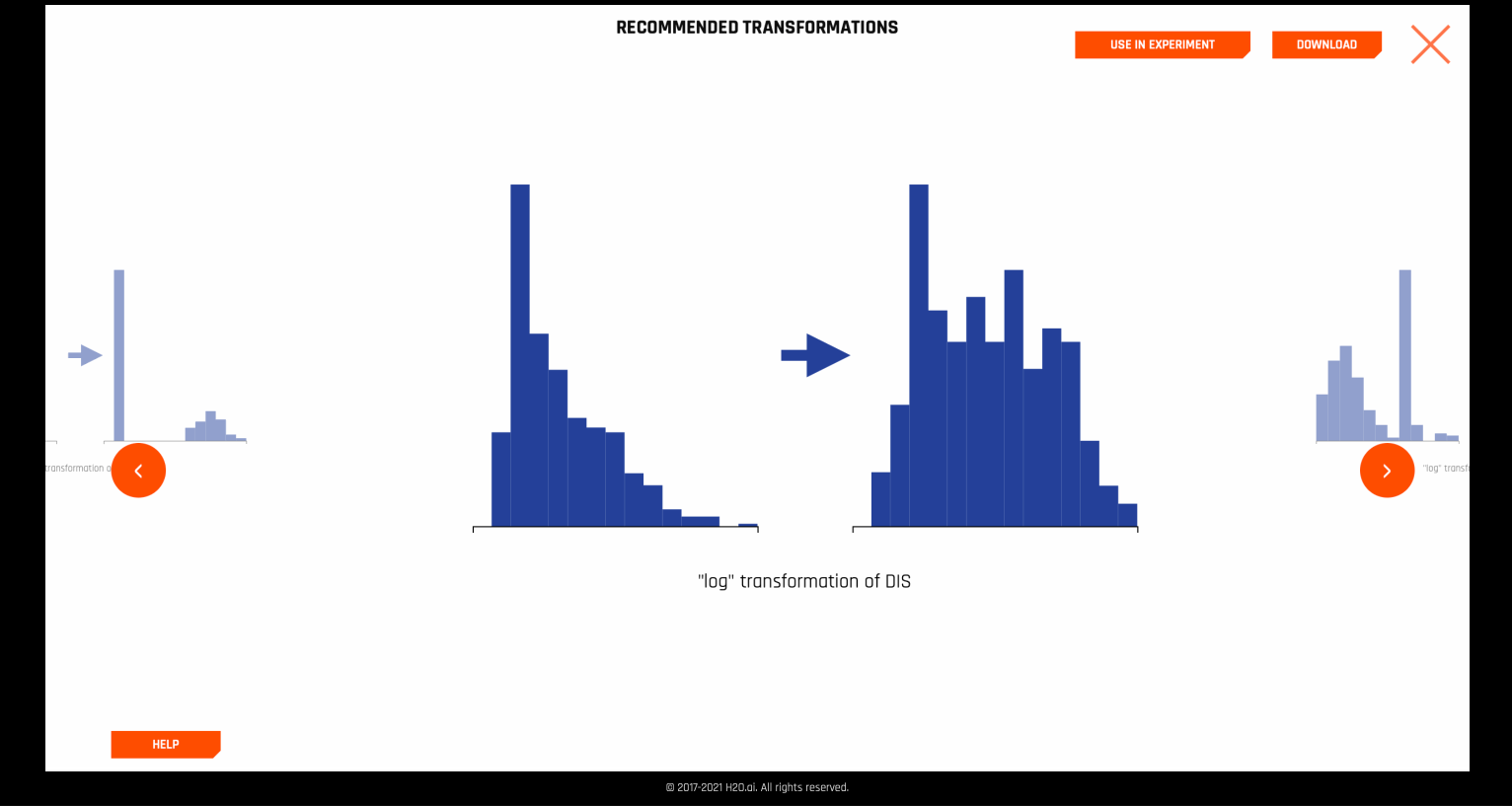
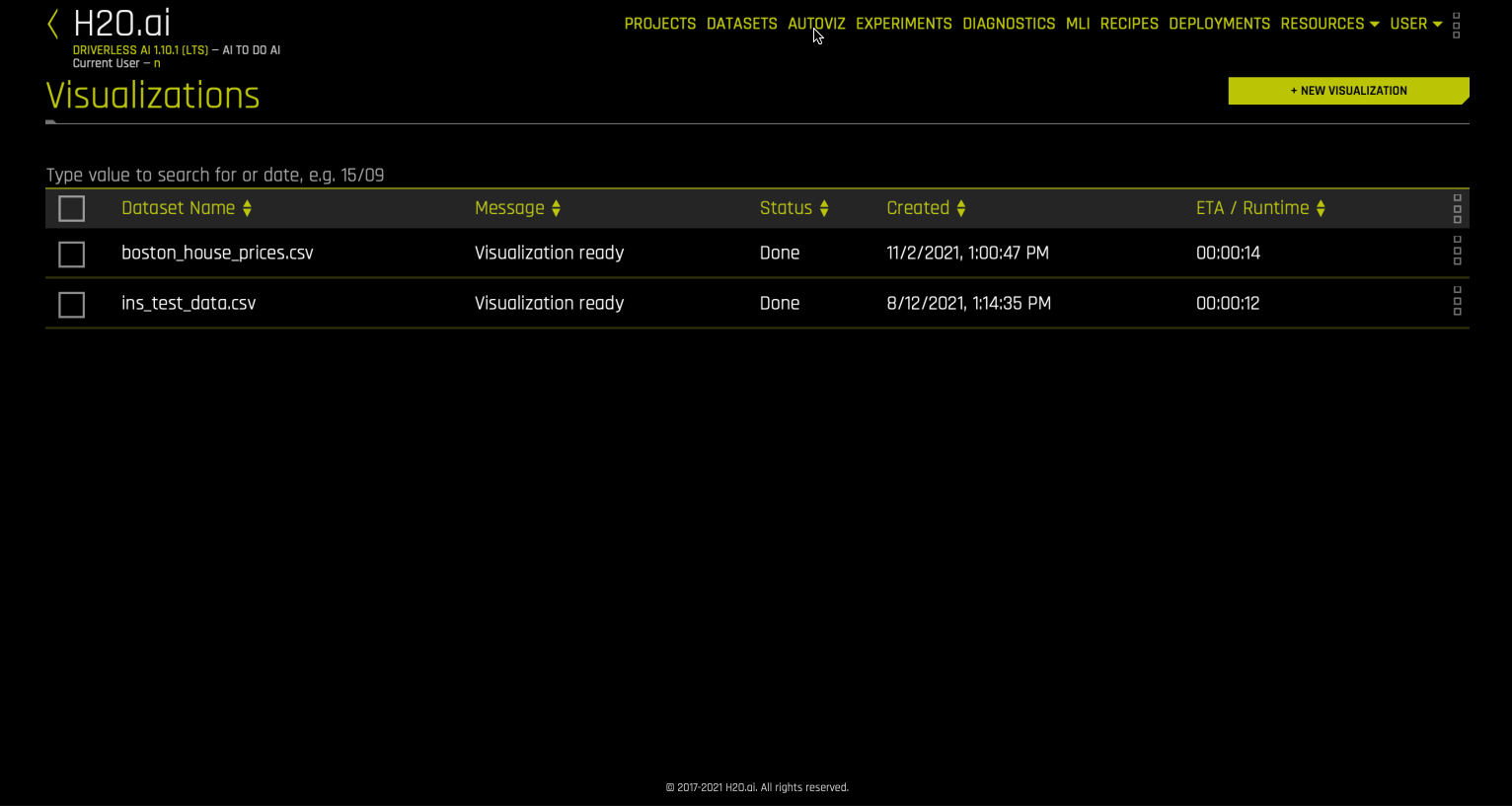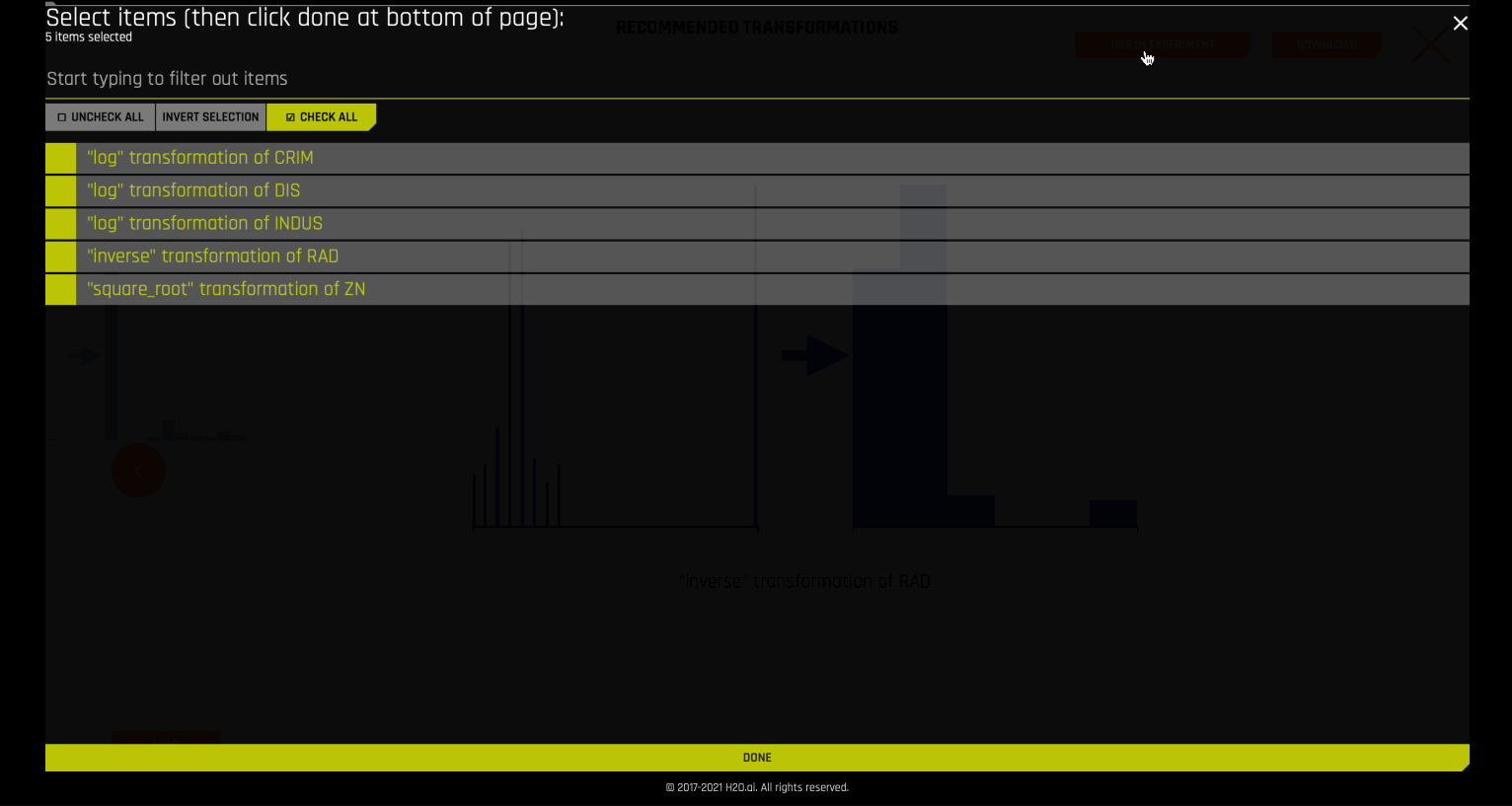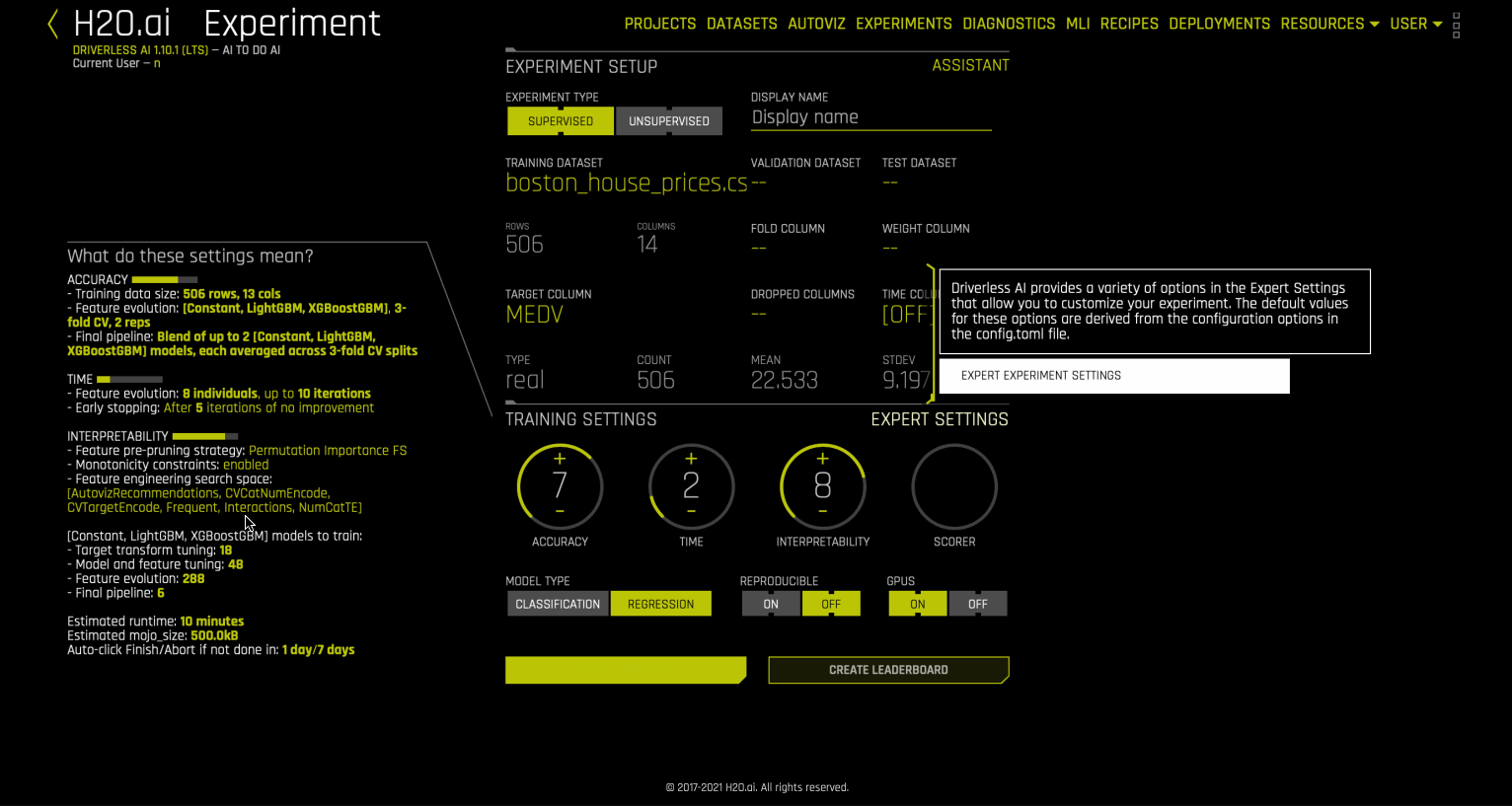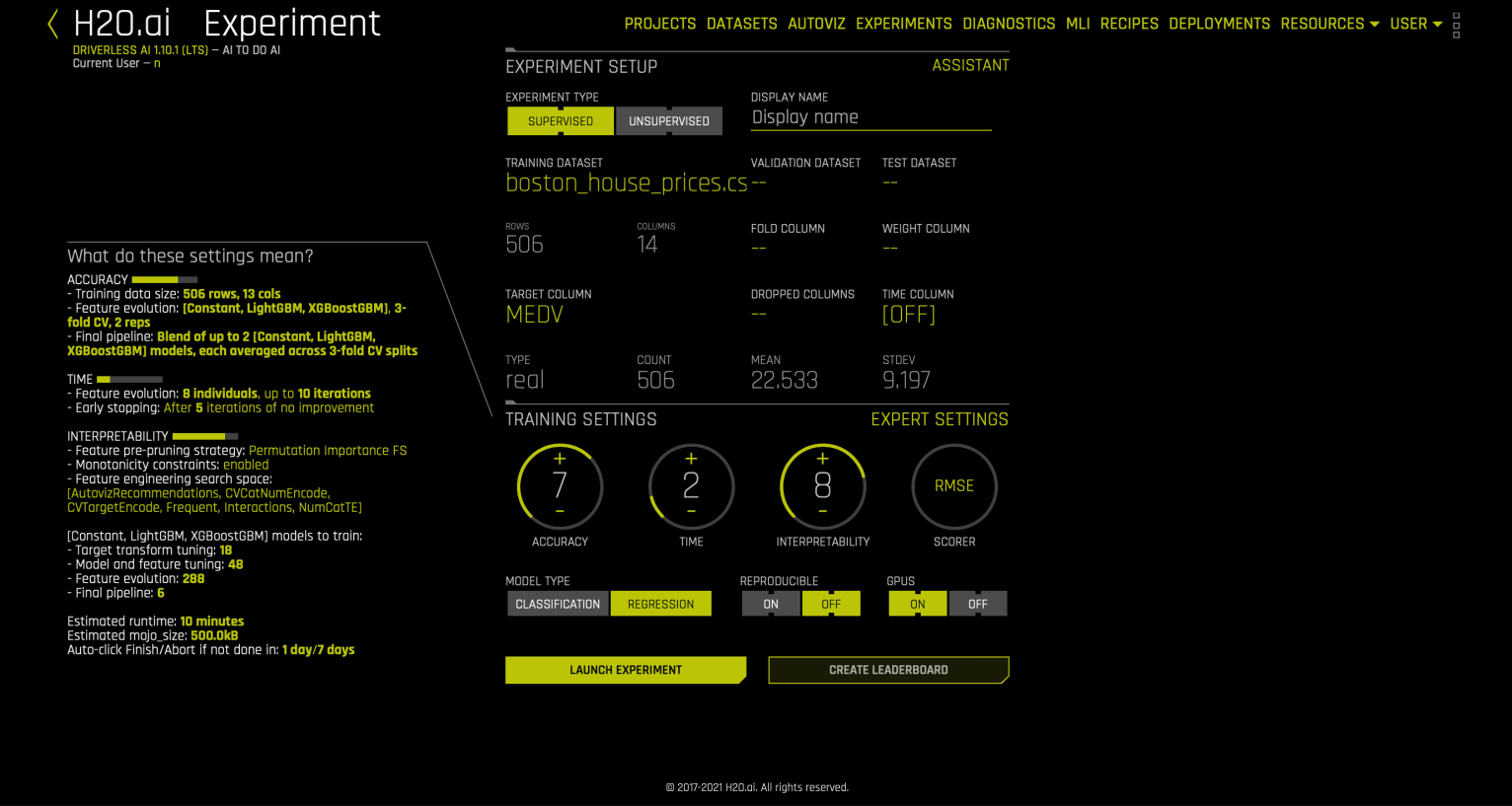
경우에 따라 Autoviz는 데이터 세트의 열에 대한 특정한 변환을 권장합니다.
이러한 권장 사항은 실험에 직접 적용할 수 있으며, autoviz recommendation transformer 를 사용하여 내부적으로 수행합니다.
다음은 Driverless AI Autoviz에서 사용할 수 있는 그래프의 전체 목록입니다.
Spikey Histograms(스파이키 히스토그램)¶
Spikey Histograms는 거대한 스파이크를 가진 히스토그램입니다. 이것은 종종 단일 값(보통 0) 또는 매우 유사한 값의 과도한 수를 나타냅니다. 《spikeyness》의 기준은 모든 bin의 평균 빈도의 10배인 bin 빈도입니다. 스파이크 변수를 통해 모델링(특히 회귀 분석 모델)하는 경우에 특히 주의해야 합니다.
Skewed Histograms¶
Skewed Histograms은 특별히 큰 왜도(비대칭성)를 가진 히스토그램입니다. 왜도의 견고한 측정은 Groeneveld, R.A. and Meeden, G. (1984), 《Measuring Skewness and Kurtosis.》 The Statistician, 33, 391-399로부터 유래되었습니다. 고도로 치우친 변수는 모델링에 사용하기 전에 변환(예: 로깅)의 후보가 될 때가 많습니다. 출력의 히스토그램은 왜도의 내림차순으로 정렬됩니다.
Varying Boxplots¶
Varying boxplots는 범주형 변수의 범주에서 특성의 비정상적인 가변성을 드러냅니다. 가변성 측정은 견고한 일원 분산분석(ANOVA)에서 계산됩니다. ANOVA에는 충분히 다양한 변수가 표시됩니다. boxplot은 분포의 분위수를 그래픽으로 나타낸 것입니다. 박스의 중심은 중앙값을 나타내고, box의 가장자리는 하위 및 상위 사분위수를 나타내며 《whiskers》의 끝단은 값의 범위를 나타냅니다. 때때로 outliers가 발생하여 인접한 whiskers가 다음 하한 또는 상한 값으로 축소됩니다. 값이 적은 변수(특성)의 경우 박스를 압축할 수 있고, 때때로 중앙값에서 단일 수평선으로 압축할 수도 있습니다.
Heteroscedastic Boxplots¶
Heteroscedastic boxplots는 범주형 변수의 범주에서 특성의 비정상적인 가변성을 나타냅니다. 이분산성은 Brown-Forsythe test: Brown, M. B. 및 Forsythe, A. B. (1974), 《Robust tests for equality of variances. Journal of the American Statistical Association, 69, 364-367을 사용하여 계산되었습니다. 플롯은 이분산성 값에 따라 순위가 정해집니다. boxplot은 분포의 분위수를 그래픽으로 나타낸 것입니다. 박스의 중심은 중앙값을 나타내고, 박스의 가장자리는 하위 및 상위 사분위수를 나타내며 《whiskers》의 끝단은 값의 범위를 나타냅니다. 때때로 outliers가 발생하여 인접한 whiskers가 다음 하한 또는 상한값으로 축소됩니다. 값이 적은 변수(특성)의 경우 박스를 압축할 수 있고, 때때로 중앙값에서 단일 수평선으로 압축할 수도 있습니다.
Biplots¶
Biplot은 포인트와 벡터를 모두 사용해서 데이터 행렬의 행과 열에 대한 구조를 동시에 나타내는 향상된 scatterplot입니다. 행은 포인트(scores)로 표시되고 열은 벡터(로딩)로 표시됩니다. 플롯은 변수(특성) 상관 행렬의 첫 두 주요소로부터 계산됩니다. outliers 또는 비정규 분포를 드러낼 수 있는 포인트에서 비정상적인(타원이 아닌) 모양을 찾아야 합니다. 그리고 제대로 분리된 보라색 벡터를 찾아야 합니다. 겹치는 벡터는 변수 사이의 높은 상관 관계를 나타낼 수 있습니다.
Outliers¶
변칙적이거나 outliers를 포함한 변수는 dotplot에서 빨간색 포인트로 표시됩니다. dotplot는 Wilkinson, L. (1999). 《Dot plots.》 The American Statistician, 53, 276–281의 알고리즘을 사용하여 구성됩니다. 모든 변칙적인 포인트가 outliers는 아닙니다. 때때로 알고리즘은 비어있는 리전에 놓여 있는 포인트에 플래그를 지정합니다(즉, 다른 포인트 근처에 있지 않음). outliers를 검사하여 코딩이 잘못되었는지 또는 기타 실수로 발생한 것인지를 확인해야 합니다. outliers는 일반적으로 발생에 관한 합리적인 설명이 존재하는 경우에만 모델에서 제거해야 합니다.
Correlation Graph¶
상관관계 그래프는 변수(특성) 사이의 모든 쌍 제곱 상관관계로부터 구성됩니다. 연속-연속 변수 쌍의 경우, 사용된 통계는 제곱 피어슨 상관관계입니다. 연속-범주형 변수 쌍의 경우, 통계는 제곱 intraclass correlation(ICC)에 기초합니다. 이 통계는 일원 분산분석(ANOVA)의 평균 제곱에서 계산됩니다. 해당 공식은 (MSbetween - MSwithin)/(MSbetween + (k - 1)MSwithin)이며, 여기서 k는 범주형 변수의 범주 수입니다. 범주형-범주형 쌍의 경우, 해당 통계는 Cramer의 V 제곱으로부터 계산됩니다. 첫 번째 변수가 k1 범주를 갖고 두 번째 변수가 k2 범주를 갖는 경우, 값의 joint frequencies에서 k1 x k2 테이블이 생성됩니다. 이 표에서 카이 제곱 통계를 계산합니다. Cramer의 V 제곱 통계는 (chi-square / n) / min(k1,k2)이며, 여기서 n은 표에 있는 joint frequencies의 합계입니다. 이러한 각각의 큰 통계 값을 포함한 변수는 네트워크 다이어그램에서 서로 인접하여 나타납니다. connecting edge에 사용되는 색상 스케일은 낮음(파란색)에서 높음(빨간색)으로 이어집니다. 짧은 빨간색 edge에 의해 연결된 변수는 높은 상관관계를 갖는 경향이 있습니다.
Parallel Coordinates Plot¶
parallel coordinates plot은 여러 변수의 비교에 사용되는 그래프입니다. 각 변수는 플롯에서의 자체 수직축을 가지고 있습니다. 각 프로파일은 단일 관찰을 위해 축의 값을 연결합니다. 데이터가 클러스터를 포함한 경우, 이러한 프로파일은 클러스터 번호로 색상이 지정됩니다.
Radar Plot(레이더 플롯)¶
레이더 플롯은 여러 변수의 비교에 사용되는 2차원 그래프입니다. 각 변수는 그래프 중심에서 시작하는 자체 축을 가지고 있습니다. 해당 데이터는 변수 사이의 값을 비교할 수 있도록 0과 1 사이의 각 변수에 대해 표준화되어있습니다. 일반적으로 star의 형태로 나타나는 각 프로파일은 단일 관측에 대한 축의 값을 연결합니다. 다변량 outliers는 빨간색 프로파일로 표시됩니다. Radar Plot은 대중적인 parallel coordinates plot의 극 버전입니다. 극 레이아웃을 사용하면 단일 플롯에서 더 많은 변수를 나타내는 것이 가능합니다.
Data Heatmap¶
heatmap 그래픽은 전치된 데이터 행렬로 구성됩니다. heatmap의 행은 변수를 나타내고 열은 케이스(인스턴스)를 나타냅니다. 데이터는 표시되기 전에 표준화되어 작은 값은 노란색, 큰 값은 빨간색입니다. 행과 열은 데이터 행렬의 특이값 분해(SVD)를 통해 치환되기 때문에 유사한 행 및 열이 서로 근접하여 위치합니다.
Recommendations¶
Recommendations 그래픽은 Exploratory Data Analysis (Tukey, 1977)에 설명된 로그, 제곱근 및 역 데이터 변환에 대한 Tukey ladder of powers 컬렉션을 구현합니다. 또한 I.K. Yeo and R.A. Johnson, “A new family of power transformations to improve normality or symmetry.》 Biometrika, 87(4), (2000)에서 유래한 음수값을 처리하는 이 세 개의 트랜스포머의 확장도 구현됩니다. 각 트랜스포머의 경우, 변환은 변환된 열의 견고한 왜도와 기존 원시 열의 견고한 왜도의 비교를 통해 선택됩니다. 변형이 상대적으로 낮은 왜도 값으로 이어지는 것이 권장됩니다.
Missing Values Heatmap¶
missing values heatmap 그래픽은 전치된 데이터 행렬로 구성됩니다. heatmap의 행은 변수를 나타내고 열은 케이스(인스턴스)를 나타냅니다. 데이터는 값 0(결측) 및 1(비결측)으로 코딩됩니다. 결측값은 빨간색으로 표시되고 비결측값은 공백(흰색)으로 표시됩니다. 행과 열은 데이터 행렬의 특이값 분해(SVD)를 통해 치환되기 때문에 유사한 행 및 열이 서로 근접하여 위치합니다.
Gaps Histogram(Gaps 히스토그램)¶
Gaps 지수는 John Tukey의 작업을 기초로 Wainer 및 Schacht 알고리즘을 이용해서 계산됩니다(Wainer, H. and Schacht, Psychometrika, 43, 2, 203-12.). Gaps를 포함한 히스토그램은 데이터 세트에서 꼭 특징지어지지는 않은 가능한 하위 그룹을 기반으로 둘 이상의 분포의 혼합을 나타낼 수 있습니다.
이 페이지의 이미지는 섬네일입니다. 그래프 중 하나를 클릭하여 실물 크기 이미지를 보고 다운로드할 수 있습니다. 확장된 각 그래프의 좌측 하단에 있는 Help 버튼을 클릭하여 각 그래프에 대한 설명을 확인할 수도 있습니다.