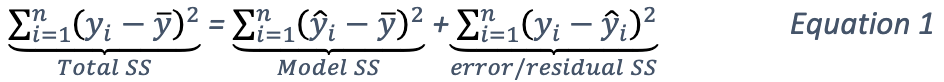ANOVA GLM¶
Introduction¶
H2O ANOVA GLM is used to calculate Type III SS (sum of squares) which is used to investigate the contributions of individual predictors and their interactions to a model. Predictors or interactions with negligible contributions to the model will have high p-values while those with more contributions will have low p-values. We use predictors to express individual predictors or interactions of predictors.
Since ANOVA GLM is mainly used to investigate the contribution of each predictor or interaction, scoring, MOJO, and cross-validation are not supported.
Defining an ANOVA GLM Model¶
Parameters are optional unless specified as requried. ANOVA GLM shares many GLM parameters.
Algorithm-specific parameters¶
highest_interaction_term: This option limits the number of interaction terms (i.e.
2means interaction between 2 columns only,3for three columns, etc.). This option defaults to2.nparallelism: Set the number of models to build in parallel (adjust according to your system). This option defaults to
4.save_transformed_framekeys: Enable this option to save the keys of transformed predictors and interaction columns. This option defaults to
False(disabled).type: Refer to the SS type 1, 2, 3, or 4. We are currently only supporting type 3.
Common parameters¶
balance_classes: (Applicable only for classification) Specify whether to oversample the minority classes to balance the class distribution. This option can increase the data frame size. Majority classes can be undersampled to satisfy the
max_after_balance_sizeparameter. This option defaults toFalse(disabled).class_sampling_factors: (Applicable only if
balance_classes=True) Specify the per-class (in lexicographical order) over/under-sampling ratios. By default, these ratios are automatically computed during training to obtain the class balance.early_stopping: Specify whether to stop early when there is no more relative improvement on the training or validation set. This option defaults to
False(disabled).ignore_const_cols: Specify whether to ignore constant training columns since no information can be gained from them. This option defaults to
True(enabled).ignored_columns: (Python and Flow only) Specify the column or columns to be excluded from the model. In Flow, click the checkbox next to a column name to add it to the list of columns excluded from the model. To add all columns, click the All button. To remove a column from the list of ignored columns, click the X next to the column name. To remove all columns from the list of ignored columns, click the None button. To search for a specific column, type the column name in the Search field above the column list. To only show columns with a specific percentage of missing values, specify the percentage in the Only show columns with more than 0% missing values field. To change the selections for the hidden columns, use the Select Visible or Deselect Visible buttons.
max_after_balance_size: (Applicable only if
balance_classes=True) Specify the maximum relative size of the training data after balancing class counts. The value can be > 1 and defaults to5.0.max_iterations: Specify the number of training iterations. This option defaults to
0.max_runtime_secs: Maximum allowed runtime in seconds for model training. This option defaults to
0(unlimited).missing_values_handling: Specify how to handle missing values. One of:
Skip,MeanImputation(default), orPlugValues.model_id: Specify a custom name for the model to use as a reference. By default, H2O automatically generates a destination key.
offset_column: Specify a column to use as the offset. This will be added to the combination of columns before applying the link function.
score_each_iteration: Specify whether to score during each iteration of the model training. This option is set to
False(disabled) by default.seed: Specify the random number generator (RNG) seed for algorithm components dependent on randomization. The seed is consistent for each H2O instance so that you can create models with the same starting conditions in alternative configurations. This option defaults to
-1(time-based random number).standardize: Specify whether to standardize the numeric columns to have a mean of zero and unit variance. This option defaults to
True(enabled).stopping_metric: Specify the metric to use for early stopping. The available options are:
AUTO(default): (This defaults tologlossfor classification anddeviancefor regression)devianceloglossMSERMSEMAERMSLEAUC(area under the ROC curve)AUCPR(area under the Precision-Recall curve)lift_top_groupmisclassificationmean_per_class_error
stopping_rounds: Stops training when the option selected for
stopping_metricdoesn’t improve for the specified number of training rounds, based on a simple moving average. This option defaults to0(no early stopping). The metric is computed on the validation data (if provided); otherwise, training data is used.stopping_tolerance: Specify the relative tolerance for the metric-based stopping to stop training if the improvement is less than this value. This option defaults to
0.001.training_frame: Required Specify the dataset used to build the model.
NOTE: In Flow, if you click the Build a model button from the
Parsecell, the training frame is entered automatically.weights_column: Specify a column to use for the observation weights, which are used for bias correction. The specified
weights_columnmust be included in the specifiedtraining_frame.Python only: To use a weights column when passing an H2OFrame to
xinstead of a list of column names, the specifiedtraining_framemust contain the specifiedweights_column.Note: Weights are per-row observation weights and do not increase the size of the data frame. This is typically the number of times a row is repeated, but non-integer values are supported as well. During training, rows with higher weights matter more, due to the larger loss function pre-factor.
x: Specify a vector containing the names or indices of the predictor variables to use when building the model. If
xis missing, then all columns exceptyare used.y: Required Specify the column to use as the dependent variable. The data can be numeric or categorical.
Type III SS¶
To demonstrate what Type III SS is and how it is implemented, here is an example of regression with two categorical predictors:
note: This algorithm will support multiple categorical/numerical columns and other families as well; we just need to replace the SS with the residual deviance for other families.
SS (Sum of Squares)¶
In Analysis of Variance (ANOVA), the partition of the response variable sum of squares in a linear model is described as “explained” and “unexplained” components. Consider a dataset generated by
\[y_i = x^T_i\beta + \epsilon_i\]
where
\(y_i\) is the response variable;
\(x^T_i = [1,x_{i1},...,x_{im}]\) are the predictors;
\(\beta = [\beta_0, \beta_1,..., \beta_m]\) are the system parameters;
\(\epsilon_i {\text{ ~ }} N(0,\sigma^2)\).
The total sum of squares of this dataset can be decomposed as follows:
where
\(\bar{y} = {\frac{1}{n}}{\sum^n_{i=1}}y_i\);
\(\hat{y_i} = x^T_i \hat{\beta} {\text{ and }} \hat{\beta} = (X^TX)^{-1}X^TY, X = {\begin{bmatrix}1^T \\ x^T_1 \\ x^T_2 \\ ... \\ X^T_m\end{bmatrix}}, Y = {\begin{bmatrix}y_1 \\ ... \\ y_n\end{bmatrix}}\).
Generally, addition of a new predictor to a model will increase the model SS and reduce the error or residual SS.
The model SS by itself is not useful. However, if you have multiple models, the difference in model SS between two models can be used to determine model performance gain/loss.
Type III SS Calculation¶
The Type III SS calculation can be illustrated using two predictors (C,R). Let
\(SS(C,R,C:R)\) denote the model sum of squares for GLM with predictors C,R and the interaction of C and R;
\(SS(C,R)\) denote the model sum of squares for GLM with predictors C,R only;
\(SS(R,C:R)\) denote the model sum of squares for GLM with predictors R and the interaction of C and R;
\(SS(C,C:R)\) denote the model sum of squares for GLM with predictors C and the interaction of C and R.
Type III SS calculation refers to the incremental sum of squares by taking the difference between the model sum of squares for alternative models:
\(SS(C|R,C:R) = SS(C,R,C:R) - SS(R,C:R) = error SS(R,C:R) - error SS(C,R,C:R)\);
\(SS(R|C,C:R) = SS(C,R,C:R) - SS(C,C:R) = error SS(C,C:R) - error SS(C,R,C:R)\);
\(SS(C:R|R,C) = SS(C,R,C:R) - SS(R,C) = error SS(R,C) - error SS(C,R,C:R)\).
The second part of the equations can be derived from Equation 1. Note that the \(error SS\) is just the residual deviance of the models.
The same procedure applies if there are more predictors. In general, to calculate the Type III SS, we build the model with all the predictors and all the predictor interactions and compare the full model to taking out either one predictor or one interaction. For example, if there are three predictors (R,C,S), then all of the following predictors can be found in the model: R, C, S, R:C, R:S, C:S, R:C:S. Hence, we calculate the difference in SS of the full model with one predictor out of the seven predictors left out. In addition, to control the number of predictors in the interaction, the parameter highest_interaction_term is added to limit the number of predictors involved in an interaction. Using the example of three predictors, if highest_interaction_term=2, the predictors used in building the full model will only be R, C, S, R:C, R:S, C:S. The interaction term R:C:S will be excluded for it has 3 predictors which is not allowed in this case.
The calculation of the SS difference is then used to estimate how important the predictor that is left out is. To do this, F-tests are used. Using the example of two categorical predictors R with r levels, C with c levels, the following table will be generated for a dataset of n rows:
Source |
Degree of freedom |
Model SS |
Hypothesis |
F |
|---|---|---|---|---|
R |
\(r-1\) |
\(SS(R|C,R:C)\) |
Coefficients for R are zero. |
\({\frac{SS(R|C,R:C)(n-r*C)}{(r-1)*errorSS}}\) |
C |
\(c-1\) |
\(SS(C|R,R:C)\) |
Coefficients for C are zero. |
\({\frac{SS(C|R,R:C)(n-r*c)}{(c-1)*errorSS}}\) |
R:C Interaction |
\((r-1)*(c-1)\) |
\(SS(R:C|R,C)\) |
Coefficients for interaction R:C are zero. |
\({\frac{SS(R:C|R,C)(n-r*c)}{(r-1)(c-1)*errorSS}}\) |
Residual SS |
\(n-r*c\) |
\(errorSS\) of full model |
||
Total: |
\(n-1\) |
Finally, to answer the question that certain coefficients should be zero, we calculate the p-value from the F-tests just like the p-value calculation with a Gaussian distribution. In this case, we assume that the distribution of F is the F statistic. If the p-value calculated is small, you reject the hypothesis that the set of parameters associated with a predictor should be set to zero.
Examples¶
library(h2o) h2o.init() # Import the prostate dataset: train <- h2o.importFile("http://s3.amazonaws.com/h2o-public-test-data/smalldata/prostate/prostate_complete.csv.zip") # Set the predictors and response: x <- c("AGE", "VOL", "DCAPS") y <- "CAPSULE" # Build and train the model: anova_model <- h2o.anovaglm(y = 'CAPSULE', x = c('AGE','VOL','DCAPS'), training_frame = train, family = "binomial", missing_values_handling="MeanImputation") # Check the model summary: summary(anova_model)import h2o h2o.init() from h2o.estimators import H2OANOVAGLMEstimator #Import the prostate dataset train = h2o.import_file("http://s3.amazonaws.com/h2o-public-test-data/smalldata/prostate/prostate_complete.csv.zip") # Set the predictors and response: x = ['AGE','VOL','DCAPS'] y = 'CAPSULE' # Build and train the model: anova_model = H2OANOVAGLMEstimator(family='binomial', lambda_=0, missing_values_handling="skip") anova_model.train(x=x, y=y, training_frame=train) # Get the model summary: anova_model.summary()