评分器¶

分类或回归¶

GINI （基尼系数）¶

基尼系数是用来量化各频率分布值之间不均等性的行之有效的方法，可以用于衡量二元分类器的质量。基尼系数为零表示完美均等（或分类器完全无用），而基尼系数为 1 则表示最大的不均等性（或分类器达到最优性能）

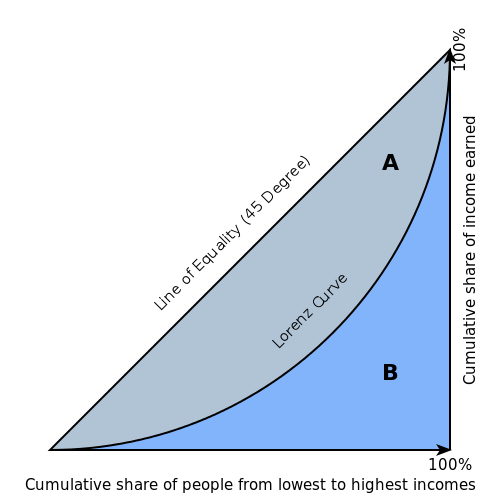
基尼系数基于洛伦兹曲线。在洛伦兹曲线图中，真正例率（y 轴）为人口百分位数的函数（x 轴）。

洛伦兹曲线呈现了分类器代表的一系列模型。特定模型的概率阈值决定了其在曲线上的位置。（即分类的概率阈值越低，真正例就越多，假正例越少。）

基尼系数本身与模型无关，只取决于洛伦兹曲线，后者由通过分类器获得的评分（或概率）的分布确定。

回归¶

R2 （R 平方）¶

R2 值表示预测值与实际值的相关性。R2 值在 0 至 1 的范围内变动，其中 0 表示预测值与实际值之间无相关性，而 1 表示完全相关。

计算线性模型的 R2 值在数学上等效于 \(1 - SSE/SST\) （或 \(1 - \text{residual sum of squares}/\text{total sum of squares}\)). 对于所有其他模型，这种等效性并不成立，因此不能使用 \(1 - SSE/SST\) 公式。在某些情况下，此公式可以得出负的 R2 值，在数学上，实数不可能出现这种情况。由于 Driverless AI 不一定使用线性模型，因此会使用皮尔逊相关系数的平方来计算 R2 值。

R2 方程：

\[R2 = \frac{\sum_{i=1}^{n}(x_i-\bar{x})(y_i-\bar{y})}{\sqrt{\sum_{i=1}^{n}(x_i-\bar{x})^2\sum_{i=1}^{n}(y_i-\bar{y})^2}}\]

其中：

x 为预测目标值
y 为实际目标值

MSE （均方误差）¶

MSE 指标用于衡量误差或偏差平方值的平均值。MSE 取从各个点到回归线的距离（这些距离为“误差”），并对它们进行平方，以剔除任何负值。MSE 结合了预测因子的方差和偏差。

MSE 还为更大的偏差赋予更大的权重。误差越大，罚分越高。例如，如果您的正确答案为 2、3、4，算法猜测的答案为 1、4、3，则每个答案的绝对误差刚好为 1，因此，平方误差也为 1，MSE 为 1。但是如果算法猜测的答案为 2、3、6，则误差为 0、0、2，平方误差为 0、0、4，而 MSE 则更大，为 1.333。MSE 越小，模型的性能越好。（提示：MSE 对异常值敏感。如果您想要更可靠的指标，可尝试平均绝对误差 (MAE)。）

MSE 方程：

\[MSE = \frac{1}{N} \sum_{i=1}^{N}(y_i -\hat{y}_i)^2\]

RMSE （均方根误差）¶

RMSE 指标用于评估模型预测连续值的性能。RMSE 的单位与预测目标的单位相同，这便于了解误差大小是否相关。RMSE 越小，模型的性能越好。（提示：RMSE 对异常值敏感。如果您想要更可靠的指标，可尝试平均绝对误差 (MAE)。）

RMSE 方程：

\[RMSE = \sqrt{\frac{1}{N} \sum_{i=1}^{N}(y_i -\hat{y}_i)^2 }\]

其中：

N 是对应数据帧的总行数（总观测次数）。
y 为实际目标值。
\(\hat{y}\) 为预测目标值。

RMSLE （均方根对数误差）¶

此指标用于衡量实际值与预测值的比率，将取预测值与实际值的对数。如果预测结果偏低比预测结果偏高要差，则使用此指标而非 RMSE。当两个值都为大数值时，如果不想对较大的差值给出罚分，您也可以使用此指标。

RMSLE 方程：

\[RMSLE = \sqrt{\frac{1}{N} \sum_{i=1}^{N} \big(ln \big(\frac{y_i +1} {\hat{y}_i +1}\big)\big)^2 }\]

其中：

N 是对应数据帧的总行数（总观测次数）。
y 为实际目标值。
\(\hat{y}\) 为预测目标值。

RMSPE （均方根百分比误差）¶

此指标为用百分比表示的 RMSE。RMSPE 越小，模型的性能越好。

RMSPE 方程：

\[RMSPE = \sqrt{\frac{1}{N} \sum_{i=1}^{N} \frac{(y_i -\hat{y}_i)^2 }{(y_i)^2}}\]

MAE （平均绝对误差）¶

平均绝对误差为绝对误差的平均值。MAE 的单位与预测目标的单位相同，这便于了解误差大小是否相关。MAE 越小，模型的性能越好。（提示：MAE 对异常值不太敏感。如果您想要对异常值敏感的指标，可尝试均方根误差 (RMSE)。）

MAE 方程：

\[MAE = \frac{1}{N} \sum_{i=1}^{N} | x_i - x |\]

其中：

N 为误差总数
\(| x_i - x |\) 等于绝对误差数。

MAPE （平均绝对百分比误差）¶

MAPE 以百分比的形式衡量误差的大小，计算为无符号百分比误差的平均值。

MAPE 方程：

\[MAPE = \big(\frac{1}{N} \sum \frac {|Actual - Forecast |}{|Actual|} \big) * 100\]

由于 MAPE 采用百分比的形式，因此指示了不同尺度之间误差的大小。参考以下示例：

实际值	预测值	绝对误差	绝对百分比误差
5	1	4	80%
15,000	15,004	4	0.03%

两个记录的绝对误差都为 4，但是将其与实际值比较时，可能认为此误差 “较小” 或 “较大” 。

SMAPE （对称平均绝对百分比误差）¶

与 MAPE（将绝对误差除以绝对实际值）不同，SMAPE 则是除以绝对实际值与绝对预测值的平均值。当实际值可能为 0 或接近 0 时，这种方法非常重要。实际值接近 0 会导致 MAPE 值变得无限大。由于 SMAPE 包括了实际值和预测值，SMAPE 值绝对不会大于 200%。

参考以下示例：

实际值	预测值
0.01	0.05
0.03	0.04

此数据的 MAPE 为 216.67%，但 SMAPE 仅为 80.95%。

两个记录的绝对误差都为 4，但是将其与实际值比较时，可能认为此误差 “较小” 或 “较大” 。

MER（平均误差率、平均绝对百分比误差）¶

MER 以百分比的形式衡量误差的中位数大小，计算为无符号百分比误差的中值。

MER 方程：

\[MER = \big(median \frac {|Actual - Forecast |}{|Actual|} \big) * 100\]

由于 MER 为中值，被评分的人口中有一半都具有比 MER 更小的绝对百分比误差，一半的人口具有比 MER 更大的绝对百分比误差。

分类¶

MCC（马修斯相关系数）¶

MCC 指标的目标将模型的混淆矩阵表示为一个数值。MCC 指标使用下述方程将真正例、假正例、真负例和假负例组合在一起。

Driverless AI 会返回概率而非预测类。为了将概率转换为预测类，需定义阈值。Driverless AI 会对可能的阈值进行迭代，以计算每个阈值的混淆矩阵。这样做的目的是找出最大的 MCC 值。Driverless AI 的目标是进一步增大此最大 MCC 值。

与准确度等指标不同，MCC 是一个不错的评分器，当目标变量不平衡时可以使用。如果数据不平衡，可以通过预测多数类来发现高准确度。尤其是在数据不平衡的情况下，准确度和 F1 等指标会存在误导性，因为它们并没有考虑四个混淆矩阵类别的相对大小。另一方面，MCC 考虑了每个类的比例。MCC 值的范围为 -1至 1，其中，-1 表示分类器预测的类与实际值预测相反类，0 表示分类器的性能并不优于随机猜测，1 表示分类器的性能最优。

MCC 方程：

\[MCC = \frac{TP \; x \; TN \; - FP \; x \; FN}{\sqrt{(TP+FP)(TP+FN)(TN+FP)(TN+FN)}}\]

F05、F1 和 F2¶

Driverless AI 模型会返回概率而非预测类。为了将概率转换为预测类，需定义阈值。Driverless AI 会对可能的阈值进行迭代，以计算每个阈值的混淆矩阵。这样做的目的是找出最大的 F 指标值。Driverless AI 的目标是进一步增大此最大 F 指标值。

F1 得分用于衡量二元分类器对正例分类的性能（在给定阈值条件下）。通过精确率率和召回率的调和平均数计算 F1 得分。F1 评分为 1 表示精确率和召回率都为最佳值，模型能正确识别所有正例，没有将负例标记为正例。如果精确率或召回率非常低，F1 评分则会更接近 0。

F1 方程：

\[F1 = 2 \;\Big(\; \frac{(precision) \; (recall)}{precision + recall}\; \Big)\]

其中：

精确率 表示模型从被其标记为正值的所有观测值中正确识别出的正观测值（真正例）（真正例个数 + 假正例个数）数量。
召回率 表示模型从所有实际正例中正确识别出的正观测值（真正值）（真正例个数 + 假正值个例）数量。

F0.5 评分为（在给定阈值条件下）精确率和召回率的加权调和平均数。与为精确率和召回率赋予相等权重的 F1 评分不同，F0.5 评分为精确率赋予了比召回率更大的权重。如果认为假正例比假负例差，则应为精确率赋予更大的权重。例如，如果用例的目的是预测您将用完哪些产品，则可以认为假正例比假负例差。在这种情况下，您就会希望预测结果非常准确，只捕捉肯定会用完的产品。如果您预测某个产品需要补充库存但实际却没有，则会因已经购买比实际需要的数量更多的存货而产生成本。

F05 方程：

\[F0.5 = 1.25 \;\Big(\; \frac{(precision) \; (recall)}{0.25 \; precision + recall}\; \Big)\]

其中：

精确率 表示模型从被其标记为正值的所有观测值中正确识别出的正观测值（真正例）（真正例个数 + 假正例个数）数量。
召回率 表示模型从所有实际正例中正确识别出的正观测值（真正值）（真正例个数 + 假正值个例）数量。

F2 评分为（在给定阈值条件下）精确率和召回率的加权调和平均数。与为精确率和召回率赋予相等权重的 F1 得分不同，F2 得分为召回率赋予了比精确率更大的权重。如果认为假负例比假正例差，则应为召回率赋予更大的权重。例如，如果用例的目的是预测您将失去哪些客户，则可以认为假负例比假正例差。在这种情况下，您就会希望预测捕捉您将失去的所有客户。这些客户中可能有部分没有流失风险，但给他们更多的关注并不会带来什么坏处。更重要的是，不会遗漏任何存在流失风险的客户。

F2 方程：

\[F2 = 5 \;\Big(\; \frac{(precision) \; (recall)}{4\;precision + recall}\; \Big)\]

其中：

精确率 表示模型从被其标记为正值的所有观测值中正确识别出的正观测值（真正例）（真正例个数 + 假正例个数）数量。
召回率 表示模型从所有实际正例中正确识别出的正观测值（真正值）（真正例个数 + 假正值个例）数量。

准确度¶

在二元分类中，准确度是指完成的正确预测次数与完成的总预测次数之比。在多类分类中，针对某一样本预测的标签集合必须刚好与 y_true 中对应的标签集合匹配。

Driverless AI 会返回概率而非预测类。为了将概率转换为预测类，需定义阈值。Driverless AI 会对可能的阈值进行迭代，以计算每个阈值的混淆矩阵。这样做的目的是找出最大的准确率值。Driverless AI 的目标是进一步增大此最大准确率值。

准确率方程：

\[准确率 = \Big(\; \frac{\text{number correctly predicted}}{\text{number of observations}}\; \Big)\]

对数损失 (logloss)¶

对数损失指标可用于评估二项或多项分类器的性能。与 AUC 不同（其研究模型对二元目标进行分类的性能），对数损失用于评估模型的预测值（未校准的概率估算值）与实际目标值的接近程度。例如，模型是否倾向于为正类分配较大的预测值（如 .80），或模型是否表现出较差的正类识别性能，并分配了较小的预测值（如 .50）？对数损失可以是大于或等于 0 的任意值，0 表示模型正确分配了 0% 或 100% 的概率。

二元分类方程：

\[Logloss = - \;\frac{1}{N} \sum_{i=1}^{N}w_i(\;y_i \ln(p_i)+(1-y_i)\ln(1-p_i)\;)\]

多类分类方程：

\[Logloss = - \;\frac{1}{N} \sum_{i=1}^{N}\sum_{j=1}^{C}w_i(\;y_i,_j \; \ln(p_i,_j)\;)\]

其中：

N 是对应数据帧的总行数（总观测次数）。
w 是由用户定义的每行权重（默认值为 1）。
C 为分类总数（对于二元分类，C=2）。
p 是为特定行（观测）分配的预测值（未校准概率）。
y 为实际目标值。

AUC（受试者工作特征曲线下面积）¶

此模型指标用来评估二元分类模型区分真正例和假正例的性能。对于多类问题，将通过对每个类求 ROC 曲线的均平均值来计算此评分。如果您偏好宏平均值，可使用 MACROAUC。

AUC 值为 1 表示分类器达到最优性能，而 AUC 值为 5 表示分类器性能较差，其性能并不优于随机猜测。

AUCPR（P-R 曲线下面积）¶

此模型指标用来评估二元分类模型区分 P-R（精确率-召回率）对或 P-R 点的性能。通过对概率性或其他连续输出分类器使用不同的阈值可以得到这些值。AUCPR 是以给定阈值的概率衡量的精确率-召回率平均值。

AUC 与 AUCPR 之间的主要差异在于，AUC 计算 ROC 曲线下方的面积，而 AUCPR 则计算 P-R 曲线下方的面积。P-R 曲线不考虑真负例。对于不平衡的数据，大量的真负例通常会导致假正例等其他指标变化的影响显得不明显。相对于 AUC，AUCPR 对真正例、假正例和假负例要敏感得多。因此，对于高度不平衡的数据，建议使用 AUCPR 而非 AUC。

MACROAUC（受试者工作特征曲线下面积的宏平均值）¶

对于多类分类问题，通过在对每个类求 ROC 曲线的宏平均值来计算此评分（每个类一个评分）。曲线下方的面积为常数。MACROAUC 为 1 表示分类器达到最优性能，而 MACROAUC 为 5 表示分类器性能较差，并不优于随机猜测。此选项对于二元分类问题不可用。

评分器最佳实践 – 回归分析¶

在决定对回归问题使用哪个评分器时，应考虑以下问题：

是否希望评分器对异常值敏感？
评分器该采用哪种单位？

对异常值敏感

某些评分器对异常值敏感。当评分器对异常值敏感时，这意味着模型预测不能非常不准确。例如，假设您通过一个实验预测某一事件发生之前的天数。下图显示了您的预测的绝对误差。

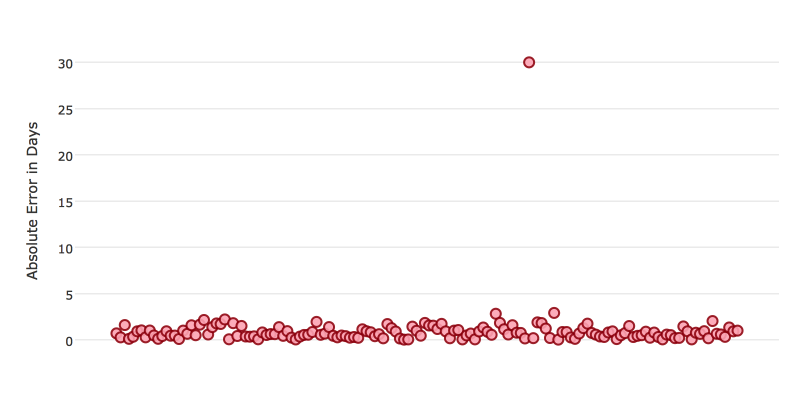
该模型通常非常有效，在约 70% 的时间里，绝对误差都小于 1 天。但是在有一个实例中，该模型表现得较差，有一次预测甚至出现了 30 天的误差。

像这样的实例会导致对异常值敏感的评分器受到更大的罚分。如果这些表现不佳的异常值不成问题，只要您通常能实现非常准确的预测，则选择对异常值不敏感的评分器。您可以看到 MSE 和 RMSE 评分器的行为反映了这一点。

	MSE	RMSE
异常值	0.99	2.64
无异常值	0.80	1.0

利用您的误差数据计算 RMSE 和 MSE ，会发现 RMSE 比 MSE 大两倍多，因为 RMSE 对异常值敏感。如果您将一个异常值记录从计算中剔除， RMSE 会明显减小。

性能单位

不同的评分器使用不同的单位表示 Driverless AI 实验的性能。本节继续使用前面的示例，目标是预测某一事件发生之前的天数。因此一些可能的性能单位有：

与目标相同：评分器的单位为天
- 例如：MAE = 5 表示模型预测的平均误差为 5 天
目标百分比：评分器的单位为天数的百分比
- 例如：MAPE = 10% 表示模型预测的平均误差为 10%
目标的平方：评分器的单位为天数的平方
- 例如：MSE = 25 表示模型预测的平均误差为 5 天（25 的平方根 = 5）

比较

指标	单位	对异常值敏感	建议
R2	范围为 0-1	否	当您希望性能在 0-1 的范围内时使用
MSE	目标的平方	是
RMSE	与目标相同	是
RMSLE	目标的对数	是
RMSPE	目标的百分比	是	当目标值使用了不同的尺度时使用
MAE	与目标相同	否
MAPE	目标的百分比	否	当目标值使用了不同的尺度时使用
SMAPE	目标值的百分比除以 2	否	当目标值接近于 0 时使用

评分器最佳实践 – 分类¶

在决定对分类问题使用哪个评分器时，应考虑以下问题：

您是否希望评分器评估预测概率或分类（可以将概率转换成这些分类）？
您的数据是否不平衡？

评分器评估概率或分类

Driverless AI 模型的最终输出是记录属于某一特定分类的预测概率。您选择的评分器评估这一概率的准确性或通过该概率进行分类的准确性。

选择标准取决于 Driverless AI 模型的使用。您是否想使用这些概率？或您是否想将这些概率转换为类？例如，如果要预测是否会流失客户，您可以取预测概率并将这些概率转换为不同类 – 将流失的客户与将不会流失的客户比较。如果要预测期望收入损失，则改为使用预测概率（预测流失概率*客户价值）。

如果用例要求为每个记录分配一个类，选择依据模型分类记录的表现来评估模型性能的评分器。如果您的用例使用概率，则选择依据预测概率评估模型性能的评分器。

对不平衡数据不敏感

对于某些用例，正类可能非常罕见。在这些实例中，某些评分器可能存在误导性。例如，如果您有一个用例，在此用例中，99% 的记录都具有 Class = No，则预测结果总是 No 的模型将具有 99% 的准确率。

对于这些用例，最佳的方法是选择不包括真负例或考虑 AUCPR 或 MCC 等真负例相对大小的指标。

比较

指标	根据以下指标进行评估	建议
MCC	类	所有类的权重都相等
F1	类	精确率和召回率的权重相等
F0.5	类	为精确率分配更大的权重，为召回率分配更小的权重
F2	类	为召回率分配更大的权重，为精确率分配更小的权重
准确度	类	高度可解释
对数损失 (logloss)	概率	优化概率
AUC	类	优化预测的排序
AUCPR	类	非常适用于不平衡数据