실험 그래프

본 섹션에서는 실행 중인 실험과 완료된 실험에 대해 표시되는 대시보드 그래프에 관해 설명합니다. 이러한 그래프는 상호작용을 합니다. 특정 포인트에 대한 자세한 내용을 확인하려면 그래프의 포인트 위로 마우스 커서를 가져갑니다.

이진 분류 실험

이진 분류 실험의 경우 Driverless AI는 ROC 곡선, Precision-Recall 그래프, 향상도 차트, Kolmogorov-Smirnov 차트 및 이득 차트를 표시합니다.

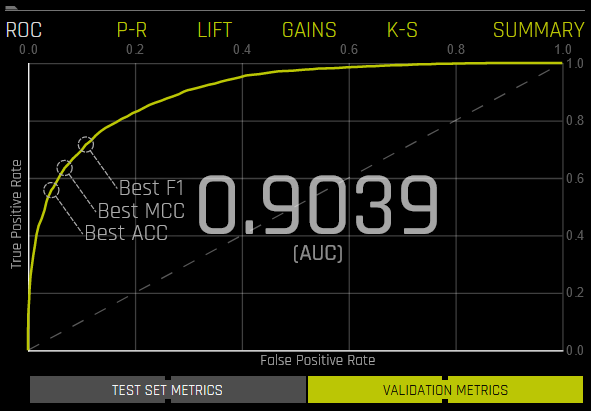
Experiment graphs

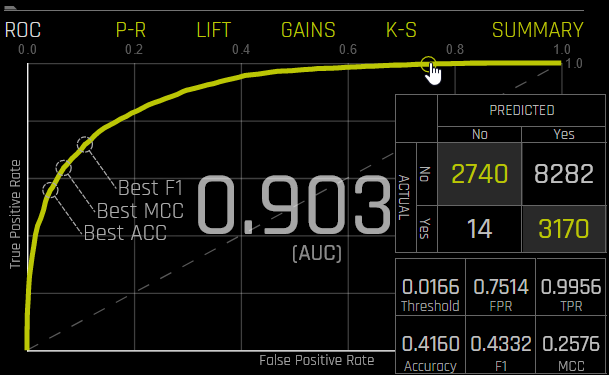
  • ROC: 이것은 최고의 accuracy, MCC 및 F1 값을 이용하여 검증 데이터에 대한 Receiver-Operator Characteristics 곡선 통계를 보여줍니다. ROC 곡선은 모델이 클래스를 얼마나 잘 구별하느냐에만 초점을 맞추기 때문에 유용한 도구입니다. 그러나 클래스 중 하나가 드물게 발생하는 모델인 경우 높은 AUC는 모델이 결과를 올바르게 예측하고 있다는 잘못된 인식을 줄 수 있습니다. 이 때문에 precision 및 recall의 개념이 중요합니다.

이 곡선의 아래 영역을 AUC라고 합니다. 참 양성률(TPR)은 정확한 양성 예측의 상대적 비율이고, 거짓 양성률(FPR)은 부정확한 양성 보정의 상대적 비율입니다. 각 포인트는 분류 임계값에 해당합니다(예: 확률이 >= 0.3이면 YES, 그렇지 않으면 NO). 각 임계값에는 TPR 및 FPR 사이의 균형을 나타내는 고유 혼동 행렬이 있습니다. 가장 유용한 작동 포인트는 일반적으로 좌측 상단에 위치합니다.

ROC 곡선의 한 포인트 위로 마우스를 커서를 가져가면, 해당 포인트에 대한 참 음성, 거짓 양성, 거짓 음성, 참 양성, 임계값, FPR, TPR, accuracy, F1 및 MCC 값을 혼동 행렬 양식으로 확인할 수 있습니다.

ROC confusion matrix

실험에 대한 테스트 세트가 제공된 경우, 그래프 아래의 Validation Metrics 버튼을 클릭하여 테스트 데이터에 대한 통계를 볼 수 있습니다.

  • Precision-Recall: 이것은 검증 데이터에 대한 Precision-Recall 곡선을 최상의 accuracy, MCC 및 F1 값과 함께 표시합니다. 이 곡선 아래의 영역을 AUCPR이라고 부릅니다. Prec-Recall은 데이터 세트에 상당한 왜곡이 있을 경우 ROC 곡선을 보완해주는 도구입니다. Prec-Recall 곡선은 가능한 모든 분류 임계값에 대해 정밀도 또는 양수 예측값(y 축) 대 민감도 또는 참 양성률(x 축)을 나타냅니다. 높은 수준에서 정밀도는 결과의 정확성 또는 품질의 척도로 생각할 수 있고, 해당 모델에서 획득한 결과의 완전성 또는 양의 척도로 재현할 수 있습니다. Prec-Recall은 모델에서 얻은 결과의 타당성을 측정합니다.

  • 정밀도: 정확한 양성 예측(TP) / 모든 양성(TP + FP).

  • 재현율: 정확한 양성 예측(TP) / 양성 예측(TP + FN).

각각의 포인트는 분류 임계값에 해당합니다(예: 확률이 0.3 이상이면 YES, 그렇지 않으면 NO). 각 임계값에는 재현율과 정밀도 사이의 균형을 나타내는 고유 혼동 행렬이 있습니다. 이 ROCPR 곡선은 불균형이 심한 데이터 세트에 대한 ROC 곡선보다 더 많은 인사이트를 줄 수 있습니다.

이 그래프의 포인트 위로 마우스의 커서를 가져가면 해당 포인트에 대한 참 양성, 참 음성, 거짓 양성, 거짓 음성, 임계값, 재현율, 정밀도, accuracy, F1 및 MCC 값을 확인할 수 있습니다.

실험에 대한 테스트 세트가 제공된 경우, 그래프 아래의 Validation Metrics 버튼을 클릭하여 테스트 데이터에 대한 통계를 볼 수 있습니다.

  • Lift: 이 차트는 검증 데이터에 대한 향상도 통계를 보여줍니다. 예를 들어, 《How many times more observations of the positive target class are in the top predicted 1%, 2%, 10%, etc. (cumulative) compared to selecting observations randomly?》. 정의에 따르면, 100%에서 향상도는 1.0입니다. 향상도는 무작위 모델(또는 모델 없음)과 비교하여 예측 모델이 얼마나 더 나은 결과를 줄 수 있는지에 대한 질문에 대한 답변에 도움을 줄 수 있습니다. 향상도는 모델 및 무작위 모델(또는 모델 없음)을 통해 얻은 결과 사이의 비율로 계산된 예측 모델의 효율성에 대한 측정입니다. 즉, 주어진 분위수에서 임의 기대 %에 대한 이득 %의 비율입니다. x 번째 분위수의 임의 기대값은 x%입니다.

향상도 차트에서 포인트 위로 마우스 커서를 가져가면, 해당 포인트에 대한 분위수 백분율 및 누적 향상도 값을 확인할 수 있습니다.

실험에 대한 테스트 세트가 제공된 경우, 그래프 아래의 Validation Metrics 버튼을 클릭하여 테스트 데이터에 대한 통계를 볼 수 있습니다.

  • Kolmogorov-Smirnov: 이 차트는 검증 또는 테스트 데이터에 대한 양성 및 음성의 분리 정도를 측정합니다.

차트의 포인트 위로 마우스의 커서를 가져가면 해당 포인트에 대한 분위수 백분율 및 Kolmogorov-Smirnov 값을 확인할 수 있습니다.

실험에 대한 테스트 세트가 제공된 경우, 그래프 아래의 Validation Metrics 버튼을 클릭하여 테스트 데이터에 대한 통계를 볼 수 있습니다.

  • Gains: 이것은 검증 데이터에 대한 이득 통계를 보여줍니다. 예를 들어, 《What fraction of all observations of the positive target class are in the top predicted 1%, 2%, 10%, etc. (cumulative)?》. 정의에 따라 100%에서의 이득은 1.0입니다.

이득 차트에서 포인트 위로 마우스 커서를 가져가면, 해당 포인트에 대한 분위수 백분율 및 누적 이득 값을 확인할 수 있습니다.

실험에 대한 테스트 세트가 제공된 경우, 그래프 아래의 Validation Metrics 버튼을 클릭하여 테스트 데이터에 대한 통계를 볼 수 있습니다.

멀티 클래스 분류 실험

멀티 클래스 분류 실험의 경우 ROC 곡선, 정밀도-재현율 그래프, 향상도 차트, Kolmogorov-Smirnov 차트 및 이득 차트 외에 혼동 행렬을 사용할 수 있습니다. Driverless AI는 멀티 클래스 문제를 여러 개의 일대 다의 문제로 간주하여 이러한 그래프를 생성합니다. 이러한 그래프와 차트(혼동 행렬 제외)는 마이크로 평균(http://scikit-learn.org/stable/auto_examples/model_selection/plot_roc.html#multiclass-settings 참조)이라는 방법을 기반으로 합니다.

예를 들어, 홍채 데이터에서 해당되는 종의 예측이 가능합니다. 해당 예측은 다음과 같습니다.

class.Iris-setosa

class.Iris-versicolor

class.Iris-virginica

0.9628

0.021

0.0158

0.0182

0.3172

0.6646

0.0191

0.9534

0.0276

이러한 차트를 생성하려면 Driverless AI는 결과를 3개의 일대다 문제로 변환합니다.

prob-setosa

actual-setosa

prob-versicolor

actual-versicolor

prob-virginica

actual-virginica

0.9628

1

0.021

0

0.0158

0

0.0182

0

0.3172

1

0.6646

0

0.0191

0

0.9534

1

0.0276

0

해당 결과는 이항 문제에 대한 예측값 및 실제값으로 구성된 3개의 벡터입니다. Driverless AI는 이 3개의 벡터를 함께 연결하여 차트를 계산합니다.

predicted = [0.9628, 0.0182, 0.0191, 0.021, 0.3172, 0.9534, 0.0158, 0.6646, 0.0276]
actual = [1, 0, 0, 0, 1, 1, 0, 0, 0]

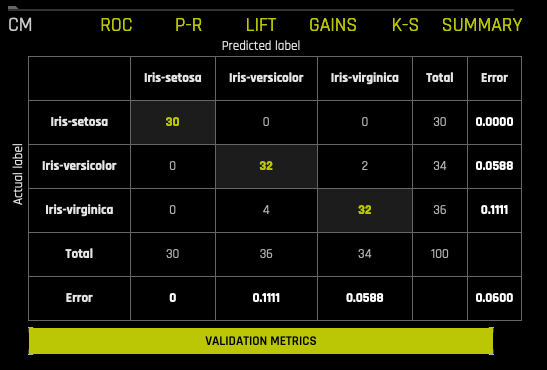
멀티 클래스 혼동 행렬

혼동 행렬은 거짓 양성, 거짓 음성, 참 양성 및 참 음성 측면에서 실험 성능을 보여줍니다. 각각의 임계값에 대한 혼동 행렬은 TPR과 FPR(ROC) 또는 정밀도와 재현율(Prec-Recall) 간의 균형을 나타냅니다. 가장 유용한 작동 지점은 일반적으로 좌측 상단에 있습니다.

이 그래프에서 실제 결과는 열에 표시되고 예측은 행에 표시됩니다. 정확한 예측은 강조 표시됩니다. 다음의 예에서 Iris-setosa 는 정확히 30회, Iris-virginica 는 정확히 32회, Iris-versicolor 는 Iris-virginica 로 2회 예측되었습니다(검증 세트 대비).

실험에 대한 테스트 세트가 제공된 경우, 그래프 아래의 Validation Metrics 버튼을 클릭하여 테스트 데이터에 대한 통계를 볼 수 있습니다.

Multiclass Confusion Matrix

회귀 분석 실험

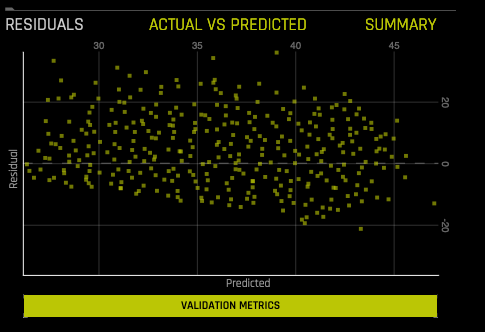
  • Residuals: Residuals 는 관측된 응답 및 모델에 의해 예측된 응답 사이의 차이입니다. 잔차의 모든 패턴은 부적절한 모델 또는 outliers와 같은 데이터의 불규칙성의 증거이며, 모델의 개선 방법을 제안합니다. 해당 차트는 검증 또는 테스트 데이터에 대한 잔차(실제 예측) 및 예측값을 나타냅니다. 이 그림은 모든 outliers를 유지합니다. 완벽한 모델의 잔차는 0입니다.

그래프의 포인트 위로 마우스의 커서를 가져가면 해당 포인트에 대한 예측값 및 잔차값을 확인할 수 있습니다.

실험에 대한 테스트 세트가 제공된 경우, 그래프 아래의 Validation Metrics 버튼을 클릭하여 테스트 데이터에 대한 통계를 볼 수 있습니다.

Residuals graph

  • Actual vs. Predicted: 이 차트는 검증 데이터의 실제값 및 예측값을 보여줍니다. 작은 값의 샘플이 표시됩니다. 완벽한 모델은 대각선을 가집니다.

그래프의 한 포인트 위로 마우스의 커서를 가져가면 해당 포인트의 실제값 및 예측값을 확인할 수 있습니다.

실험에 대한 테스트 세트가 제공된 경우, 그래프 아래의 Validation Metrics 버튼을 클릭하여 테스트 데이터에 대한 통계를 볼 수 있습니다.

Experiment graphs